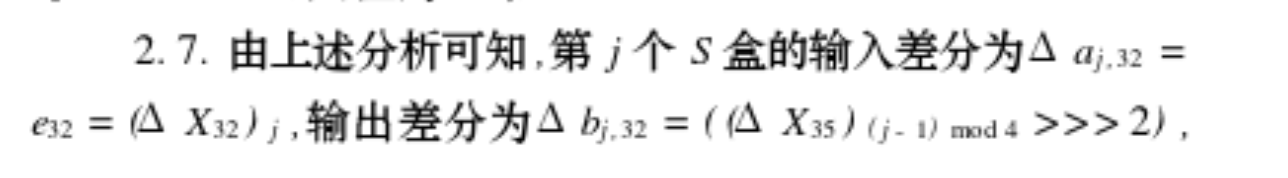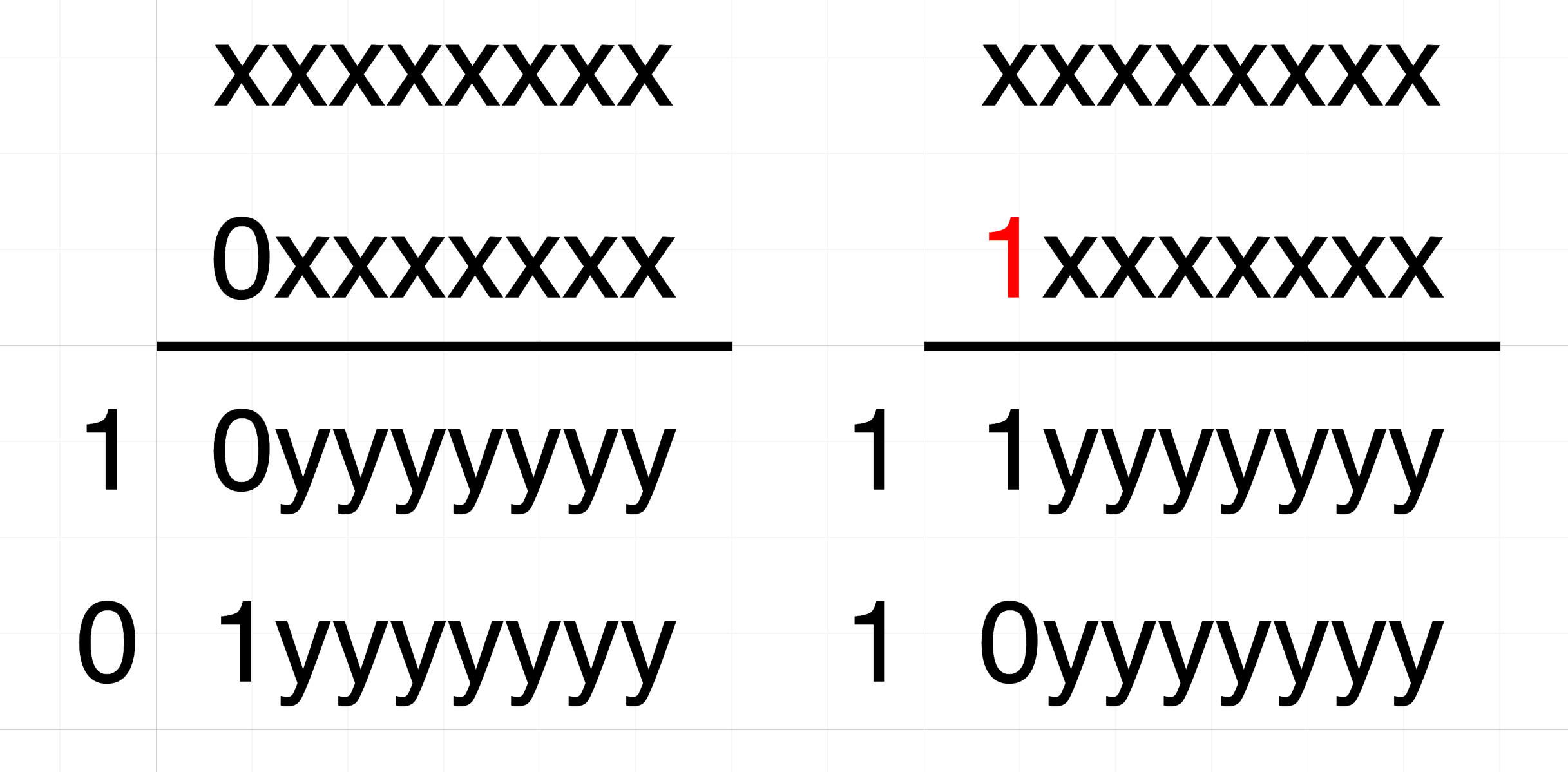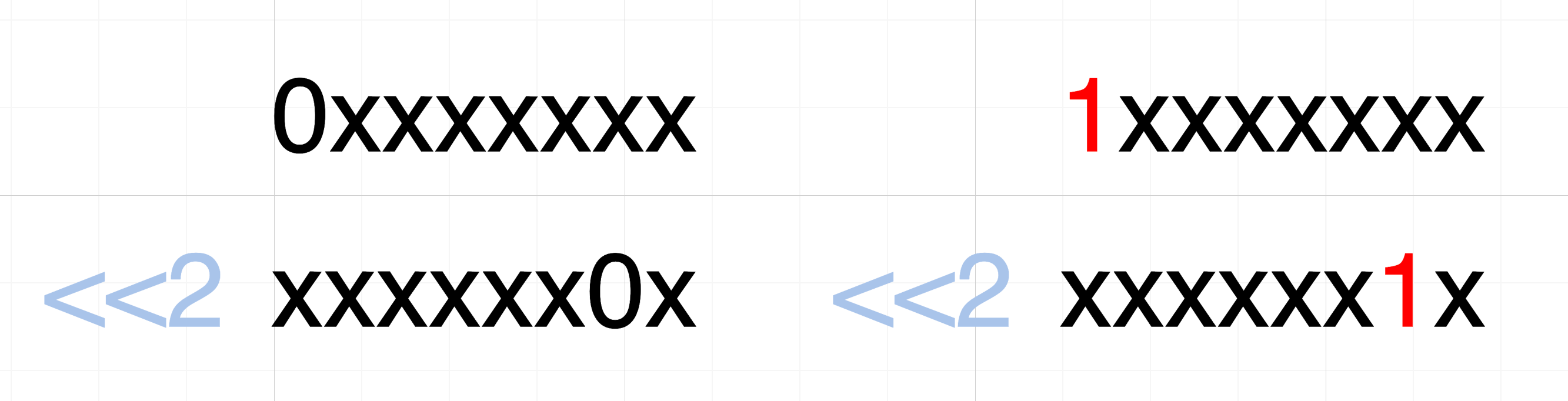(2021.11.20更新)可以看这位师傅的文章
差分攻击可以说是密码分析中的一门经典手艺了,一直想去学的,但是没什么时间(太懒了
最近比赛遇到了2个差分攻击的题目,分别是6轮DES的差分攻击(differential attack)和SM4国密算法的故障差分攻击(differential fault attack)。
差分攻击,之前也只是稍微在一篇大神写的由Feal-4密码算法浅谈差分攻击
上有所了解。
做题的时候,甚至连SM4算法是什么都不知道。
全部都是当场找paper,然后现学现卖的。
但是不得不说,真正自己去实现一遍差分攻击后,对DES、SM4算法的理解程度真的提升了很大的一截。
如何快速地去学习某个密码算法?日它!
以下是比赛题目的writeup,均首发于TEAM-SU
.
hellman yyds!
这题是淘宝师傅
出的,tttqqqlll
改过的DES 6轮差分攻击
现学:
现学材料里的一个可能疑惑点:第4轮的F函数中,有5个sbox的input(6bit)的差分值都是0,所以这5个sbox的output(4bit)的差分值也都是0,经过P置换后,得到的D’中有4*5=20bit是已知的。所以后面第6轮的F函数的output的差分值:$F’ = c’ \oplus D’ \oplus T_L’$中,有20bit是确定的;经过逆P置换后,得到第6轮8个sbox的outputs的差分值,其中有5个对应的sbox的output的差分值是已知的,所以能用medium里的那个方法把这5个sbox的key求出来。
c’为第3个F函数input的差分值,D’为第4个F函数input的差分值,F’为第6个F函数output的差分值,$T_L’$是密文左半部分的差分值。
攻击方法
DES里面就sbox比较难搞,其他的部分就是一些线性置换,可以通过一些差分特性去操作一下这个sbox,然后就能得到key。
简单来说就是,找到一个差分特征后,可以用这个特征推4轮,然后计算$F’ = c’ \oplus D’ \oplus T_L’$(第6轮F函数output的差分值),逆P置换,得到8个sbox的outputs的差分值out_xors,这个差分值的概率是最大的;接着,将2个已知的第6轮F函数的input(密文的右半部分)去做e扩展,得到$I_1, I_2$,分别分成8组${i_{11}, i_{12}, …, i_{18}}, {i_{21}, i_{22}, …, i_{28}}$,对应着8个sbox。
每一个sbox,对所有可能的64种key(6bit)作判断sbox($i_{1j}$ ^ key) ^ sbox($i_{2j}$ ^ key) == out_xors[j],如果等于,则将该key计数加1。尝试很多次后,必然有一个key出现的次数最多,且远超其他的key,该key即为正确的key。
这8个6bit的key合起来就是第6轮的subkey,又由于密钥扩展就是一个置换,可以反推出前面5轮的key。
把key反过来加密就能getflag。
手动寻找差分特征
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
from collections import Counter
...
def gen_diff_output(diff):
p1 = getRandomNBitInteger(32)
p2 = p1 ^ diff
k = getRandomNBitInteger(48)
c1, c2 = F(p1, k), F(p2, k)
return c1^c2, (p1,p2,c1,c2)
counter = Counter()
for i in range(10000):
P_ = 0x00000040
X_, _ = gen_diff_output(P_)
counter[X_] += 1
X_, freq = counter.most_common(1)[0]
print(hex(X_)[2:].rjust(8,'0'), freq / 10000)
# 0x00000002 -> 0x00000002 0.217
# 0x00000040 -> 0x00000000 0.2534
# 0x00000400 -> 0x00000000 0.251
# 0x00000000 -> 0x00000000 1
# 0x00002000 -> 0x00000000 0.25
# 0x00004000 -> 0x00000040 0.22
# 0x00020000 -> 0x00020000 0.18
|
发现了好几组非常优秀的差分特征。
选择0x00000040 -> 0x00000000 0.2534
画图分析
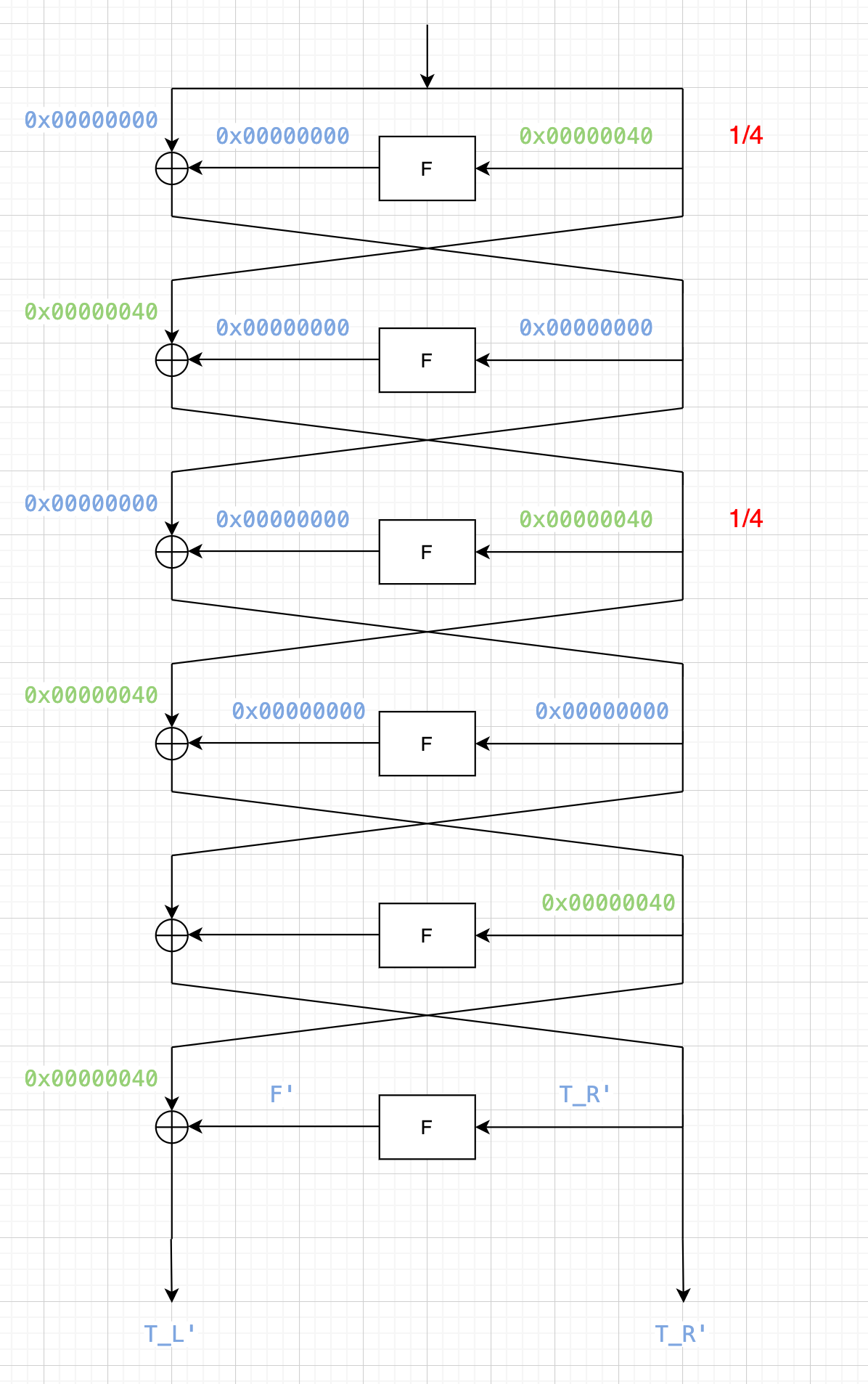
在线画图:https://draw.io
可以推出来$F’ = 0x00000040 \oplus T_L'$
获取数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import re
from json import dump
from tqdm import tqdm
from Crypto.Util.number import long_to_bytes, getRandomNBitInteger
from pwn import *
def gen_diff_input(diff):
p1 = getRandomNBitInteger(64)
p2 = p1 ^ diff
return p1, p2
r = remote("81.68.174.63", 34129)
# context.log_level = "debug"
rec = r.recvuntil(b"required").decode()
cipher_flag = re.findall(r"\n([0-9a-f]{80})\n", rec)[0]
print(cipher_flag)
r.recvline()
pairs = []
for i in tqdm(range(10000)):
p1, p2 = gen_diff_input(0x0000000000000040)
r.sendline(long_to_bytes(p1).hex().encode())
c1 = int(r.recvline(keepends=False), 16)
r.sendline(long_to_bytes(p2).hex().encode())
c2 = int(r.recvline(keepends=False), 16)
pairs.append(((p1,p2), (c1,c2)))
r.close()
dump([cipher_flag, pairs], open("data", "w"))
|
差分攻击
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
from collections import Counter
from json import load
from tqdm import tqdm
cipher_flag, pairs = load(open("data", "r"))
...
def inv_key(key):
inv_key = [0]*48
key_bin = bin(key)[2:].rjust(48, '0')
for j in range(48):
inv_key[pc_key[j]] = key_bin[j]
return int(''.join(inv_key), 2)
def inv_keys(k6):
keys = [0]*6
keys[-1] = k6
for i in range(4,-1,-1):
keys[i] = inv_key(keys[i+1])
return keys
def inv_p(x):
x_bin = [int(_) for _ in bin(x)[2:].rjust(32, '0')]
y_bin = [0]*32
for i in range(32):
y_bin[pbox[i]] = x_bin[i]
y = int(''.join([str(_) for _ in y_bin]), 2)
return y
# --------------------------
candidate_keys = [Counter() for _ in range(8)]
for _, cs in tqdm(pairs):
c1, c2 = cs
if c1 ^ c2 == 0x0000004000000000:
continue
l1, l2 = c1 >> 32, c2 >> 32
r1, r2 = c1 & 0xffffffff, c2 & 0xffffffff
# print(r1, r2)
F_ = l1^l2^0x00000040
F_ = inv_p(F_) # xor of the two outputs of sbox, 32bit
Ep1 = e(r1) # 48bit
Ep2 = e(r2) # 48bit
for i in range(8):
inp1 = (Ep1 >> (7-i)*6) & 0b111111 # 6bit
inp2 = (Ep2 >> (7-i)*6) & 0b111111 # 6bit
out_xor = (F_ >> (7-i)*4) & 0b1111 # 4bit
for key in range(64):
if s(inp1^key, i) ^ s(inp2^key, i) == out_xor:
candidate_keys[i][key] += 1
print(candidate_keys)
# ----------------------
key6 = []
for c in candidate_keys:
print(c.most_common(2))
key6.append(c.most_common(1)[0][0])
print(key6)
# key6 = [53, 44, 38, 7, 7, 30, 29, 52]
k6 = sum(key6[i]<<(7-i)*6 for i in range(8))
# k6 = 236161043654516
keys = inv_keys(k6)
print(keys)
ps, cs = pairs[0]
p1, c1 = ps[0], cs[0]
assert enc_block(p1) == c1
# Ok! key is right!
# To decrypt, reverse the keys.
keys = keys[::-1]
print(enc(bytes.fromhex(cipher_flag)))
# b'WMCTF{D1ff3r3nti@1_w1th_1di0t_B0X3s}\x00\x00\x00\x00'
|
WMCTF{D1ff3r3nti@1_w1th_1di0t_B0X3s}
代码已打包:https://mega.nz/file/jCgEiIgA#N37BzoOky4MLE-6taxoNBOR48Vloh_zdb9yeWEzK8jg
这题可惜,没抢到前3血,只是第4个做出来的。。
differential fault attack SM4
找paper:
Min WANG,Zhen WU,Jin-tao RAO,Hang LING. Round reduction-based fault attack on SM4 algorithm[J]. Journal on Communications, 2016, 37(Z1): 98-103.
这篇不太行,直接把最后的几轮给扔了,不太realistic;不过从中学到了SM4的构造,以及SM4的DFA相关研究
找到了https://eprint.iacr.org/2010/063.pdf
We show that if a random byte fault is induced into either the second, third or fourth word register at the input of the 28-th round, the 128-bit master key could be derived with an exhaustive search of 22.11 bits on average.
28轮的第2、3、4个寄存器出错,可以直接整出master key,很对头
The procedure of the round-key generation indicates that the master key can be easily retrieved from any four consecutive round-keys.
然后几个paper轮流看。

选择了需要fault次数最多的那个方法。(因为容易理解一些
paper:https://wenku.baidu.com/view/df86818e79563c1ec5da71c4.html
出题人没整好输入的round(只能在第2~31轮注入fault, 而非1~32轮),所以操作的时候就稍微需要自己改变一下
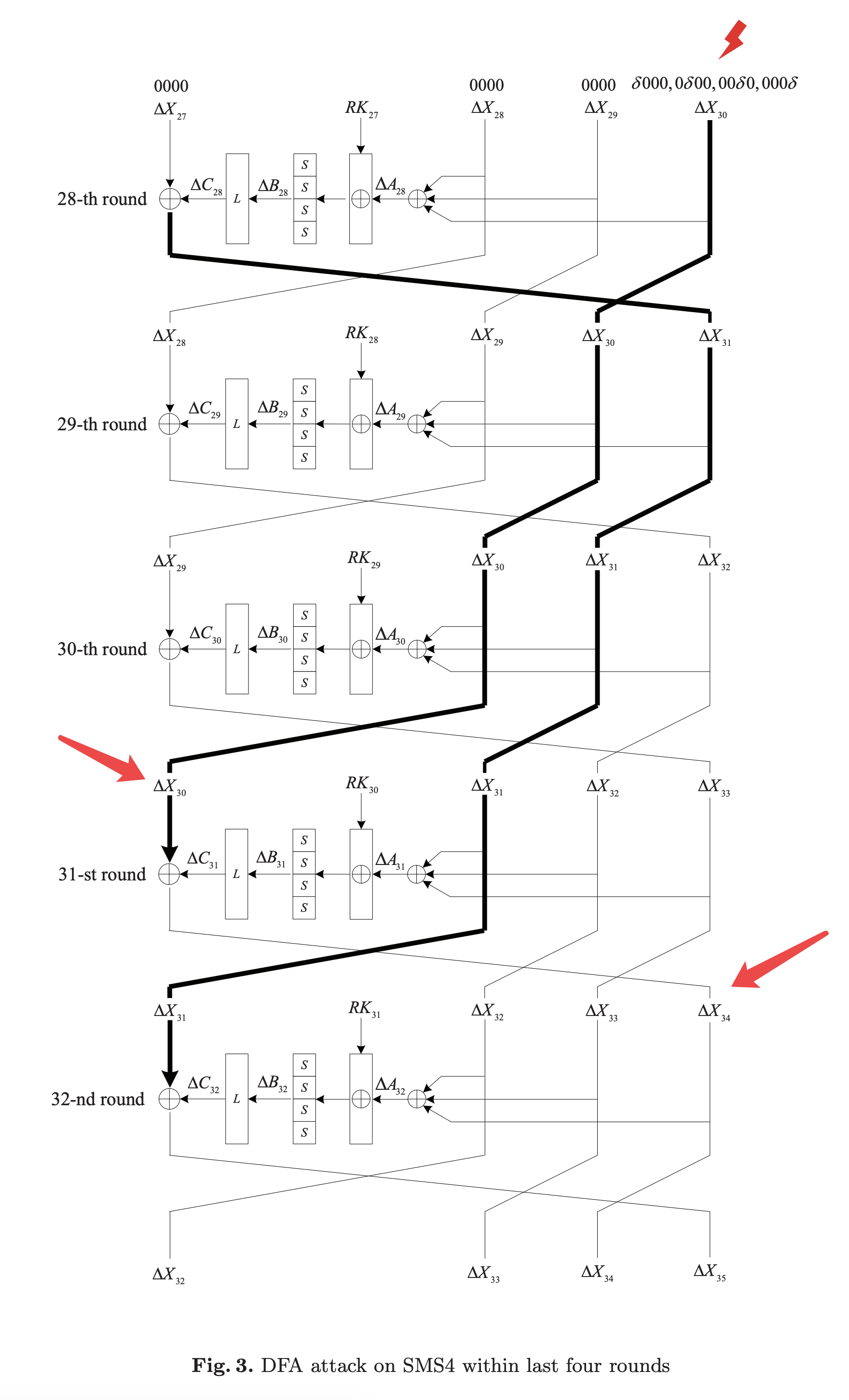
往第31轮的X30上注入1byte的fault,将会导致第32轮的X34的差分值有1byte不为0。
然后往F函数里面日:
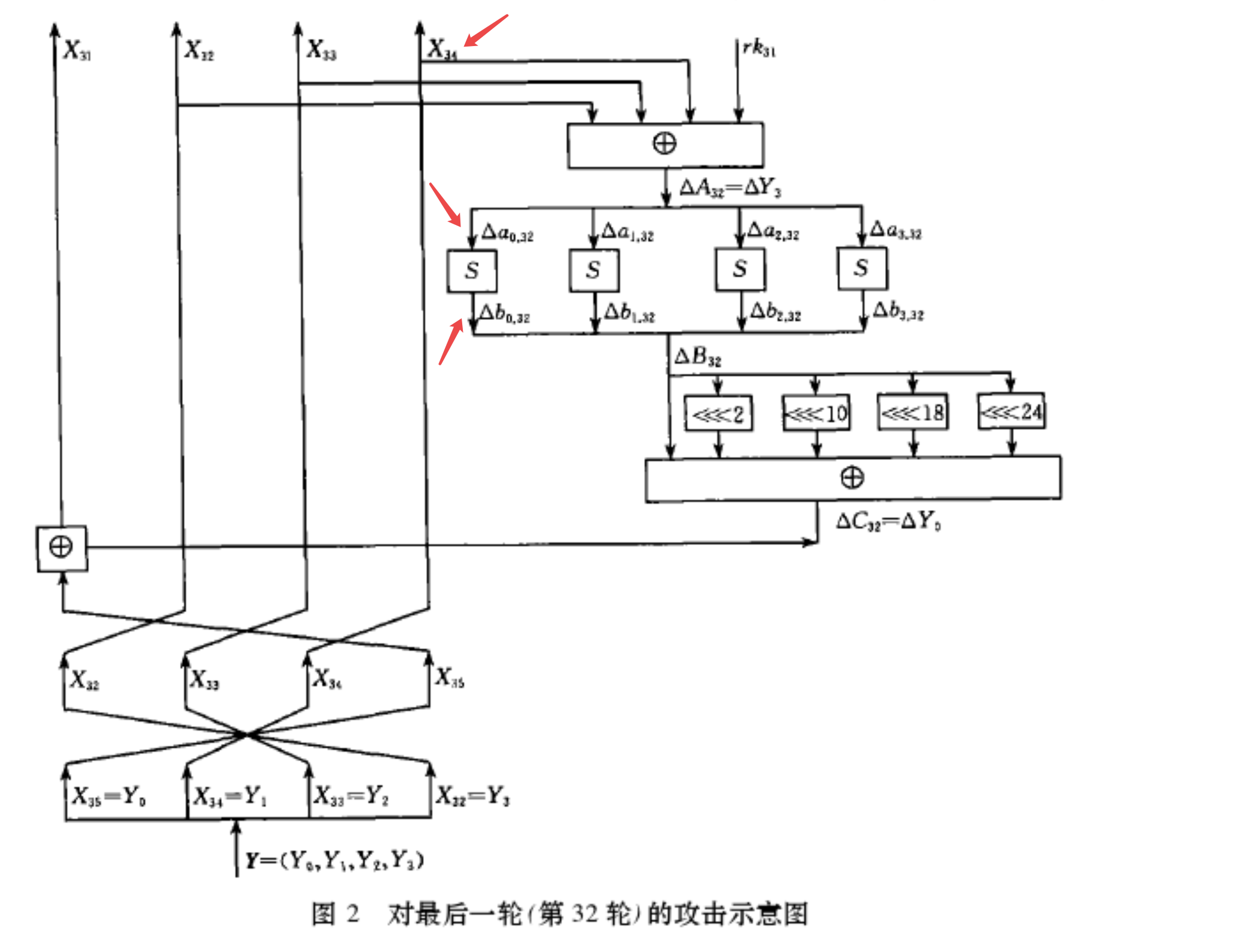
必有一个sbox的差分值不为0(其他3个sbox均为0),且这个sbox的位置可控;这个sbox的两个差分输入r_inp, f_inp 也能确定下。
r_byte: raw input byte
f_byte: fault input byte
再来从下往上看这个sbox输出的差分值:
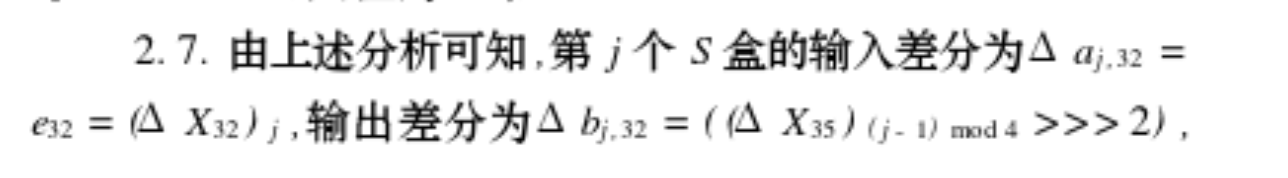
paper里有具体的分析,看不懂,直接看到结论。这个结论就是说sbox输出的差分值diff_out也能确定下来。
ok,然后穷举这个sbox所对应那一byte子密钥rk_byte(仅256种可能,一个子密钥有4byte,每1byte对应一个sbox),计算sbox(r_inp ^ rk_byte) ^ sbox(f_inp ^ rk_byte),看是否等于diff_out,如果等于就说明这个byte可以作为备选子密钥byte(理论值是说这边有2.0236个可能的子密钥byte)。两次这么操作后,基本上就可以确定下这个byte到底是哪一个了。
然后这么重复4次,分别在不同的sbox对应的位置处注入fault,即可恢复出这第32轮的4byte子密钥。
恢复出来后,可以解密一轮来到第31轮,往第30轮的X29处注入fault,等价于往第31轮的X33处注入,然后同样的操作,可以会付出这第31轮的子密钥。
再恢复2轮,即可得到第32、31、30、29轮的子密钥。
key schedule可逆,能直接搞到master key
最后解密,getflag
脚本很乱:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
|
from collections import Counter
import random
from itertools import product
from hashlib import sha256
from pwn import *
from sm4 import *
from func import xor, rotl, get_uint32_be, put_uint32_be, \
bytes_to_list, list_to_bytes, padding, unpadding
token = b"icq3f18237ca27013a7969864ab40836"
r = remote("39.101.134.52", 8006)
# context.log_level = 'debug'
# PoW
rec = r.recvline().decode()
suffix = re.findall(r'XXX\+([^\)]+)', rec)[0]
digest = re.findall(r'== ([^\n]+)', rec)[0]
print(f"suffix: {suffix} \ndigest: {digest}")
print('Calculating hash...')
for i in product(string.ascii_letters + string.digits, repeat=3):
prefix = ''.join(i)
guess = prefix + suffix
if sha256(guess.encode()).hexdigest() == digest:
print(guess)
break
r.sendafter(b'Give me XXX:', prefix.encode())
r.sendafter(b"teamtoken", token)
r.recvuntil(b"your flag is\n")
enc_flag = r.recvline().strip()
print(enc_flag)
plaintext = b"\x00" * 15
def ltor(b, l):
bits = bin(b)[2:]
return int(bits[-l:] + bits[:-l], 2)
def inv_Y(cipher):
# bytes -> list
Y0 = get_uint32_be(cipher[0:4])
Y1 = get_uint32_be(cipher[4:8])
Y2 = get_uint32_be(cipher[8:12])
Y3 = get_uint32_be(cipher[12:16])
# X32, X33, X34, X35
return [Y3, Y2, Y1, Y0]
def inv_round(Xs):
return [Xs[-1], Xs[0], Xs[1], Xs[2]]
def get_rk_byte(raw_cipher, fault_ciphers, j):
r_res, r_X32, r_X33, r_X34 = inv_round(raw_cipher)
r_byte = put_uint32_be(r_X32 ^ r_X33 ^ r_X34)[j%4]
ios = []
for f_cipher in fault_ciphers:
f_res, f_X32, f_X33, f_X34 = inv_round(f_cipher)
diff_out = ltor(put_uint32_be(r_res ^ f_res)[(j-1)%4], 2)
f_byte = put_uint32_be(f_X32 ^ f_X33 ^ f_X34)[j%4]
ios.append((f_byte,diff_out))
# print(ios)
candidate_keys = Counter()
for rk_byte in range(256):
for f_byte, diff_out in ios:
if SM4_BOXES_TABLE[r_byte^rk_byte] ^ SM4_BOXES_TABLE[f_byte^rk_byte] == diff_out:
candidate_keys[rk_byte] += 1
return candidate_keys.most_common()[0][0]
def get_r_cipher():
r.sendlineafter(b"> ", b"1")
r.sendlineafter(b"your plaintext in hex:", plaintext.hex().encode())
cipher = bytes.fromhex(r.recvline().strip().decode().split("hex:")[1])
return cipher
def get_f_cipher(round, j):
r.sendlineafter(b"> ", b"2")
r.sendlineafter(b"your plaintext in hex:", plaintext.hex().encode())
r.sendlineafter(b"give me the value of r f p:", f"{round} {random.getrandbits(8)} {j}")
cipher = bytes.fromhex(r.recvline().strip().decode().split("hex:")[1])
return cipher
def f(x0, x1, x2, x3, rk):
# "T algorithm" == "L algorithm" + "t algorithm".
# args: [in] a: a is a 32 bits unsigned value;
# return: c: c is calculated with line algorithm "L" and nonline algorithm "t"
def _sm4_l_t(ka):
b = [0, 0, 0, 0]
a = put_uint32_be(ka)
b[0] = SM4_BOXES_TABLE[a[0]]
b[1] = SM4_BOXES_TABLE[a[1]]
b[2] = SM4_BOXES_TABLE[a[2]]
b[3] = SM4_BOXES_TABLE[a[3]]
bb = get_uint32_be(b[0:4])
c = bb ^ (rotl(bb, 2)) ^ (rotl(bb, 10)) ^ (rotl(bb, 18)) ^ (rotl(bb, 24))
return c
return (x0 ^ _sm4_l_t(x1 ^ x2 ^ x3 ^ rk))
def decrypt_one_round(cipher, rk):
return [f(cipher[3], cipher[0], cipher[1], cipher[2], rk), cipher[0], cipher[1], cipher[2]]
def decrypt_rounds(cipher, rks):
for rk in rks:
cipher = decrypt_one_round(cipher, rk)
return cipher
raw_cipher = inv_Y(get_r_cipher())
print(raw_cipher)
rks = []
for round in range(31, 27, -1):
# print(round)
rk = 0
for j in range(4):
fault_ciphers = set()
for k in range(10):
fault_ciphers.add(get_f_cipher(round, j))
fault_ciphers = [inv_Y(i) for i in fault_ciphers]
fault_ciphers = [decrypt_rounds(f_cipher, rks) for f_cipher in fault_ciphers]
rk_byte = get_rk_byte(raw_cipher, fault_ciphers, j)
rk = (rk << 8) + rk_byte
print(f"round {round+1} subkey: {rk}")
rks.append(rk)
raw_cipher = decrypt_one_round(raw_cipher, rk)
def _round_key(ka):
b = [0, 0, 0, 0]
a = put_uint32_be(ka)
b[0] = SM4_BOXES_TABLE[a[0]]
b[1] = SM4_BOXES_TABLE[a[1]]
b[2] = SM4_BOXES_TABLE[a[2]]
b[3] = SM4_BOXES_TABLE[a[3]]
bb = get_uint32_be(b[0:4])
rk = bb ^ (rotl(bb, 13)) ^ (rotl(bb, 23))
return rk
# def set_key(key, mode):
# key = bytes_to_list(key)
# sk = []*32
# MK = [123, 456, 789, 145]
# k = [0]*36
# MK[0] = get_uint32_be(key[0:4])
# MK[1] = get_uint32_be(key[4:8])
# MK[2] = get_uint32_be(key[8:12])
# MK[3] = get_uint32_be(key[12:16])
# k[0:4] = xor(MK[0:4], SM4_FK[0:4])
# for i in range(32):
# k[i + 4] = k[i] ^ (
# _round_key(k[i + 1] ^ k[i + 2] ^ k[i + 3] ^ SM4_CK[i]))
# sk[i] = k[i + 4]
# return sk
def inv_key_schedule(rks):
k = [0] * 32 + rks[::-1]
for i in range(31, -1, -1):
k[i] = k[i+4] ^ (_round_key(k[i + 1] ^ k[i + 2] ^ k[i + 3] ^ SM4_CK[i]))
print(k[4:])
Mk = [0] * 4
for j in range(4):
Mk[j] = SM4_FK[j] ^ k[j]
master_key = []
for i in range(4):
master_key += put_uint32_be(Mk[i])
return list_to_bytes(master_key)
Mk = inv_key_schedule(rks)
print(Mk)
r.sendlineafter(b"> ", b"3")
r.sendlineafter(b"your key in hex:", Mk.hex().encode())
r.sendlineafter(b"your ciphertext in hex:", enc_flag)
r.recvuntil(b"your plaintext in hex:")
flag = r.recvline().strip().decode()
print(bytes.fromhex(flag))
r.interactive()
|
但是能getflag:
googlectf原题魔改了下,主要是对AES中一轮的差分攻击(除去了AddRoundKey这一步,只有SubBytes是非线性的),挺有意思的。
googlectf的writeup写的非常好: https://github.com/nguyenduyhieukma/CTF-Writeups/blob/master/Google%20CTF%20Quals/2020/oracle/oracle-solution.ipynb
只要改改第一个subchallenge的脚本,就能出:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
|
from socket import create_connection
from base64 import b64encode, b64decode
import aes # https://raw.githubusercontent.com/boppreh/aes/master/aes.py
def _xor(a, b):
assert len(a) == len(b)
return bytes(x ^ y for x, y in zip(a, b))
def _and(a, b):
assert len(a) == len(b)
return bytes(x & y for x, y in zip(a, b))
def R(x):
tmp = aes.bytes2matrix(x)
aes.sub_bytes(tmp)
aes.shift_rows(tmp)
aes.mix_columns(tmp)
return aes.matrix2bytes(tmp)
def invR(x3):
tmp = aes.bytes2matrix(x3)
aes.inv_mix_columns(tmp)
aes.inv_shift_rows(tmp)
aes.inv_sub_bytes(tmp)
return aes.matrix2bytes(tmp)
def solve_x(diff_in_1, diff_out_1, diff_in_2, diff_out_2):
# precondition for x to be unique
assert(all(diff_in_1[i] != diff_in_2[i] for i in range(16)))
# aliases
dx_1, dx_2 = diff_in_1, diff_in_2
dx3_1, dx3_2 = diff_out_1, diff_out_2
# calculate dx1_1
tmp1 = aes.bytes2matrix(dx3_1)
aes.inv_mix_columns(tmp1)
aes.inv_shift_rows(tmp1)
dx1_1 = aes.matrix2bytes(tmp1)
# calculate dx1_2
tmp2 = aes.bytes2matrix(dx3_2)
aes.inv_mix_columns(tmp2)
aes.inv_shift_rows(tmp2)
dx1_2 = aes.matrix2bytes(tmp2)
# brute-force for each component x[i]
x = bytearray(16)
for i in range(16):
xi = set()
for c in range(256):
if (
aes.s_box[c] ^ aes.s_box[c ^ dx_1[i]] == dx1_1[i] and
aes.s_box[c] ^ aes.s_box[c ^ dx_2[i]] == dx1_2[i]
):
xi.add(c)
# make sure there's a unique solution for each component
assert(len(xi) == 1)
x[i] = xi.pop()
return bytes(x)
# import os
# from aegis import _xor
# x = os.urandom(16)
# diff_in_1 = b'\x01' * 16
# diff_in_2 = b'\x02' * 16
# diff_out_1 = _xor(R(x), R(_xor(x, diff_in_1)))
# diff_out_2 = _xor(R(x), R(_xor(x, diff_in_2)))
# xx = solve_x(diff_in_1, diff_out_1, diff_in_2, diff_out_2)
# print(x, xx, x == xx)
HOST = "122.112.209.168"
PORT = 10090
_s = create_connection((HOST, PORT))
_f = _s.makefile()
# _f.readline() # ignore the welcome message
_f.readline() # ignore the IV too (knowing only the IV is useless)
def oracle1(pt, aad):
_s.sendall(b64encode(pt) + b'\n')
_s.sendall(b64encode(aad) + b'\n')
ct = b64decode(_f.readline())
tag = b64decode(_f.readline())
return ct, tag
# Step 1&2
# the original state transition parameters
p0 = p1 = p2 = b'\x00' * 16
# prepare the plaintext and associated data to be sent to the oracle
pt = p0 + p1 + p2
aad = b''
# to observe the desired key blocks, we need to make the plaintext 2-block longer
pt += b'\x00' * 16 * 2
# make the oracle call
ct, _ = oracle1(pt, aad) # the tag can be ignored
k0 = ct[16 * 0: 16 * 1]
k1 = ct[16 * 1: 16 * 2]
k2 = ct[16 * 2: 16 * 3]
k3 = ct[16 * 3: 16 * 4]
k4 = ct[16 * 4: 16 * 5]
def aegis_128l_partial_state_recover(pair1, pair2):
# assuming i = 0
ds10 = [] # ∆s[1][0]
dRs10 = [] # ∆R(s[1][0])
for pair in (pair1, pair2):
dp0, dk2 = pair
dp00, dp01 = dp0[:16], dp0[16:]
dk20, dk21 = dk2[:16], dk2[16:]
ds10.append(dp00) # ∆s[1][0] == ∆p[0][0]
dRs10.append(dk20) # ∆R(s[1][0]) == ∆k[2][0]
s10 = solve_x(ds10[0], dRs10[0], ds10[1], dRs10[1])
return s10
# Step 3
pairs = []
for dp0 in (b'\x01' * 16, b'\x02' * 16):
m = _xor(p0, dp0) + b'\x00' * 16 * 2
c, _ = oracle1(m, b'')
dk2 = _xor(k2, c[16 * 2: 16 * 3])
pairs.append((dp0, dk2))
s10 = aegis_128l_partial_state_recover(*pairs)
print(f"s10: {s10}")
# Step 4
pairs = []
for dp1 in (b'\x01' * 16, b'\x02' * 16):
m = p0 + _xor(p1, dp1) + b'\x00' * 16 * 2
c, _ = oracle1(m, b'')
dk3 = _xor(k3, c[16 * 3: 16 * 4])
pairs.append((dp1, dk3))
s20 = aegis_128l_partial_state_recover(*pairs)
pairs = []
for dp2 in (b'\x01' * 16, b'\x02' * 16):
m = p0 + p1 + _xor(p2, dp2) + b'\x00' * 16 * 2
c, _ = oracle1(m, b'')
dk4 = _xor(k4, c[16 * 4: 16 * 5])
pairs.append((dp2, dk4))
s30 = aegis_128l_partial_state_recover(*pairs)
s24 = invR(_xor(s30, s20))
s14 = invR(_xor(s20, s10))
s13 = invR(_xor(s24, s14))
print(f"s13: {s13}")
print(f"s14: {s14}")
# for _ in range(4):
# oracle1(bytes(16), b'')
# print(_f.readline())
s12 = b64decode(_f.readline().split("leak:")[1])
print(f"s12: {s12}")
# k1 = s11 ^ (s12 & s13) ^ s14
s11 = _xor(_xor(k1, _and(s12, s13)), s14)
print(f"s11: {s11}")
S = b''.join([s10, s11, s12, s13, s14])
_s.sendall(b64encode(S) + b'\n')
print(_f.readline())
print(_f.readline())
|
flag{50eec693-3014-4123-b285-361a68ab78e4}
Reference:
FEAL-4(Fast data Encipherment ALgorithm)是一个Fesitel结构(4轮)的block cipher. 两个日本人于1987年提出来的,打算用来取代DES(DES:“怎么可能?想多了”)。
The cipher is susceptible to various forms of cryptanalysis, and has acted as a catalyst in the discovery of differential and linear cryptanalysis.
64-bit输入,64-bit输出。
64-bit的key经过key schedule后,生成6个32-bit的round keys.
round keys之间似乎没有多少关系,无法从一个round key推出其他的round keys,更无法反推出64-bit的主密钥。
加密流程如下:
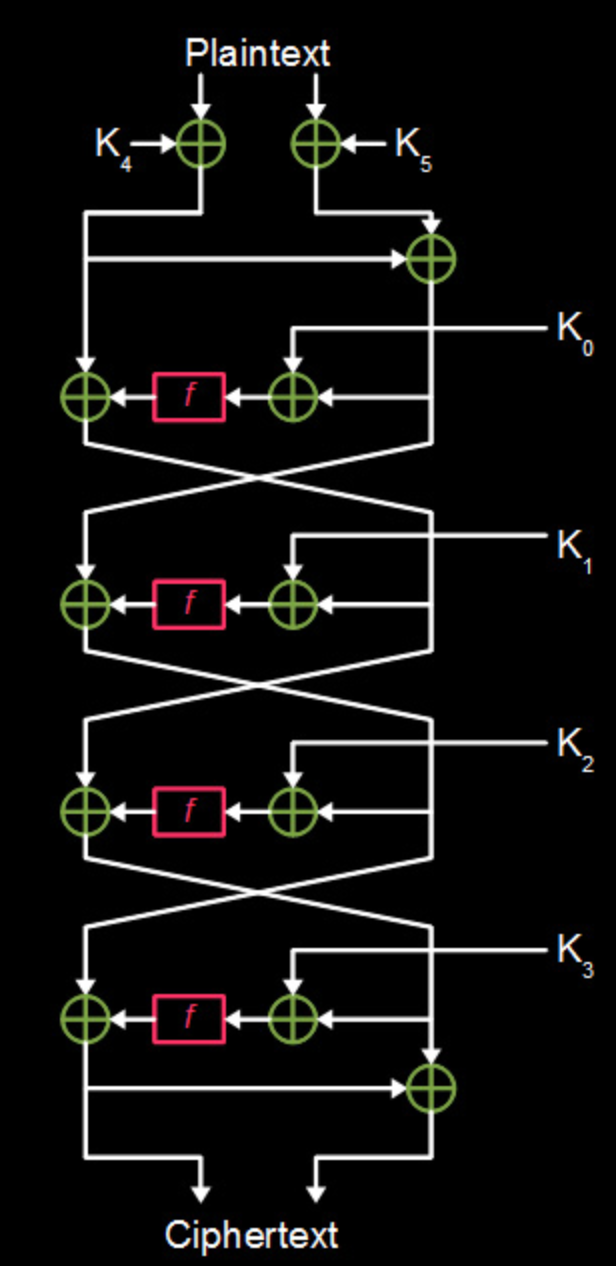
Fesitel结构,4轮操作,其中非线性的f函数是核心,其构造如下:
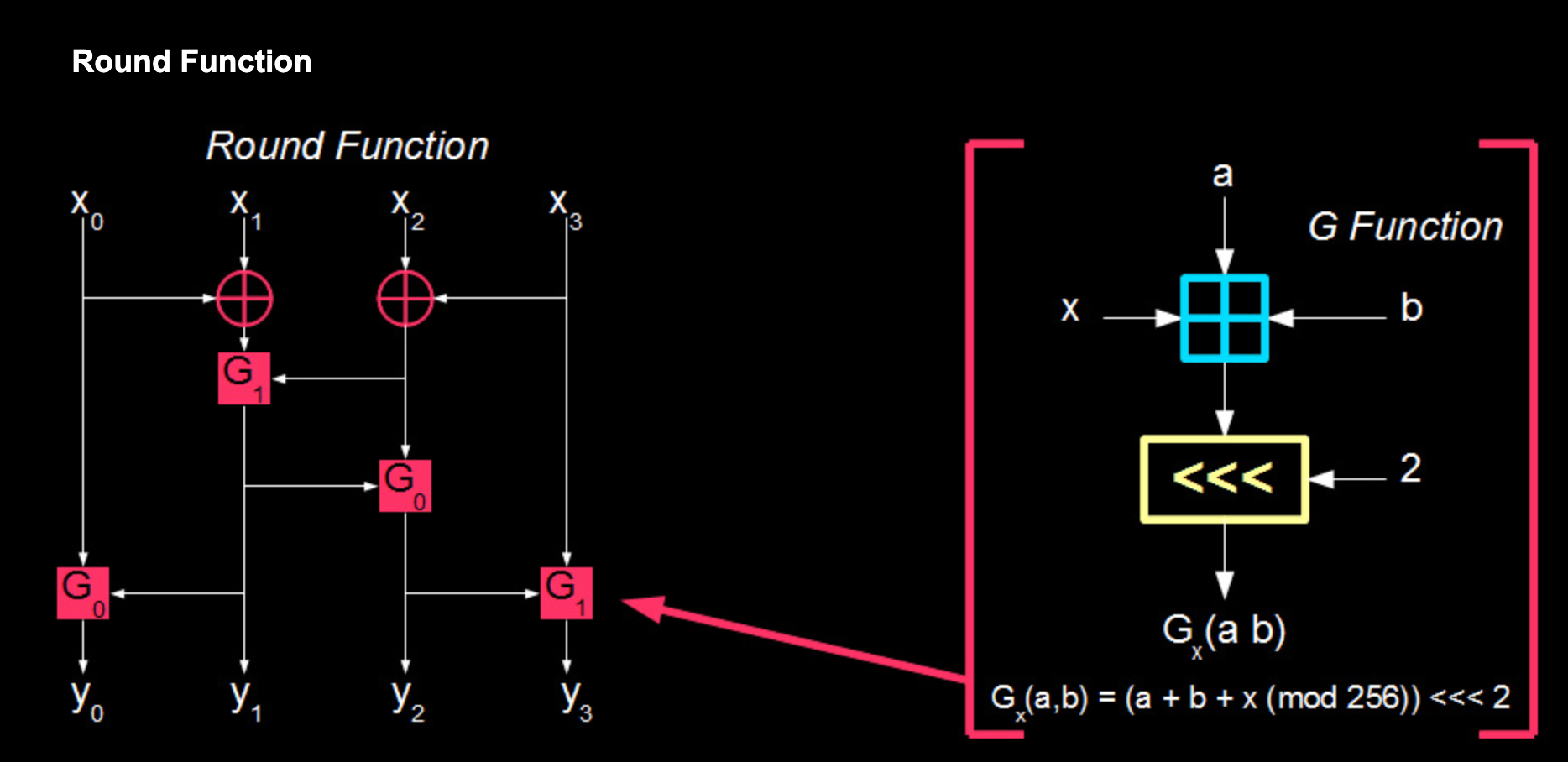
如果说f函数是FEAL-4的核心,那么G函数就是f函数的核心,G函数由一层addition modulo 256和一层cyclic left shift组成。
代码实现
Python版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
|
# -*- coding: utf-8 -*-
# AUTHOR: Soreat_u (2020-10-12)
'''
Feal-4 Symmetric Cipher Implementation.
'''
__all__ = [
'FEAL4'
]
class FEAL4():
def __init__(self, rks):
self._rks = rks
def encrypt(self, msg):
assert isinstance(msg, bytes)
assert len(msg) == 8
L = int.from_bytes(msg[:4], 'big')
R = int.from_bytes(msg[4:], 'big')
L = L ^ self._rks[4]
R = (R ^ self._rks[5]) ^ L
for r in range(3):
L, R = R, L ^ FEAL4._F(R^self._rks[r])
L = L ^ FEAL4._F(R^self._rks[3])
R = L ^ R
return L.to_bytes(4, 'big') + R.to_bytes(4, 'big')
def decrypt(self, cipher):
assert isinstance(cipher, bytes)
assert len(cipher) == 8
L = int.from_bytes(cipher[:4], 'big')
R = int.from_bytes(cipher[4:], 'big') ^ L
for r in range(3, 0, -1):
L, R = R, L ^ FEAL4._F(R^self._rks[r])
L = L ^ FEAL4._F(R^self._rks[0])
R = R ^ L
L = L ^ self._rks[4]
R = R ^ self._rks[5]
return L.to_bytes(4, 'big') + R.to_bytes(4, 'big')
@staticmethod
def _G(A, B, delta):
return FEAL4._rol2((A + B + delta) % 256)
@staticmethod
def _rol2(i):
return ((i << 2) | (i >> 6)) & 0xFF
@staticmethod
def _F(a):
A = int.to_bytes(a, 4, 'big')
G1 = FEAL4._G(A[0]^A[1], A[2]^A[3], 1)
G2 = FEAL4._G(G1, A[2]^A[3], 0)
G3 = FEAL4._G(G2, A[3], 1)
G0 = FEAL4._G(A[0], G1, 0)
return int.from_bytes(bytes([G0, G1, G2, G3]), 'big')
def test():
import os
rks = [int.from_bytes(os.urandom(4), 'big') for _ in range(6)]
# print(rks)
feal4 = FEAL4(rks)
msg = b"01234567"
cipher = feal4.encrypt(msg)
decrypted = feal4.decrypt(cipher)
print(msg, cipher, decrypted, sep="\n")
if __name__ == "__main__":
test()
|
C版本
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
|
#include <stdio.h>
#include <stdlib.h>
#define u8 uint8_t
#define u32 uint32_t
u32 combine(u8 *inp) {
return ((u32)inp[0] << 24) | ((u32)inp[1] << 16) |
((u32)inp[2] << 8) | ((u32)inp[3]);
}
void split(u32 inp, u8 *res) {
res[0] = inp >> 24;
res[1] = inp >> 16;
res[2] = inp >> 8;
res[3] = inp;
}
u8 rol2(u8 i) {
return (i << 2) | (i >> 6);
}
u8 G(u8 A, u8 B, u8 delta) {
return rol2(A + B + delta);
}
u32 F(u32 A) {
u8 A0 = A >> 24, A1 = A >> 16, A2 = A >> 8, A3 = A;
u8 tmp[4] = {0};
tmp[1] = G(A0^A1, A2^A3, 1);
tmp[2] = G(tmp[1], A2^A3, 0);
tmp[3] = G(tmp[2], A3, 1);
tmp[0] = G(A0, tmp[1], 0);
return combine(tmp);
}
void encrypt(u8 *msg, u32 *rks, u8 *res) {
u32 L = combine(msg), R = combine(msg+4);
L = L ^ rks[4];
R = (R ^ rks[5]) ^ L;
for (int r = 0; r < 3; r++) {
u32 tmp = R;
R = L ^ F(R^rks[r]);
L = tmp;
}
L = L ^ F(R^rks[3]);
R = L ^ R;
split(L, res);
split(R, res+4);
}
void decrypt(u8 *cipher, u32 *rks, u8 *res) {
u32 L = combine(cipher), R = combine(cipher+4);
R = R ^ L;
for (int r = 3; r > 0; r--) {
u32 tmp = R;
R = L ^ F(R^rks[r]);
L = tmp;
}
L = L ^ F(R^rks[0]);
R = R ^ L;
L = L ^ rks[4];
R = R ^ rks[5];
split(L, res);
split(R, res+4);
}
int main(int argc, char const *argv[]) {
u32 rks[] = {
534262442,
2244115112,
1494586470,
520548913,
2665478657,
3764657957
};
u8 msg[] = {'0', '1', '2', '3', '4', '5', '6', '7'};
u8 cipher[8] = {0};
u8 decrypted[8] = {0};
encrypt(msg, rks, cipher);
decrypt(cipher, rks, decrypted);
for (int i = 0; i < 8; i++) {
printf("%d ", cipher[i]);
}
printf("\n");
for (int i = 0; i < 8; i++) {
printf("%d ", decrypted[i]);
}
printf("\n");
return 0;
}
|
ok,该去日它了。
差分攻击,一般来说分为以下几个步骤:
- 寻找差分特征(differential characteristic)
- 构造差分路径
- 爆破子密钥
首先是要去找差分特征。
FEAL-4没有sbox,其最关键的非线性结构是最里面的G函数:模256的加法 + 循环左移2位
模256的加法,对于差分的一个障碍点在于,低位的某一bit的改变,会通过加法的进位影响到高位。
例如下图中,第一个加数不变,第二个加数的右边第4bit改变,将会导致加法结果的3bit(对应右边第4bit+高2bit)改变。

但是如果我们让第二个加数的最高位改变,那么必然会导致加法结果的最高位改变,以及(可能)carry bit的改变。但是由于取模256的操作,carry bit会被discard,不影响最终结果。
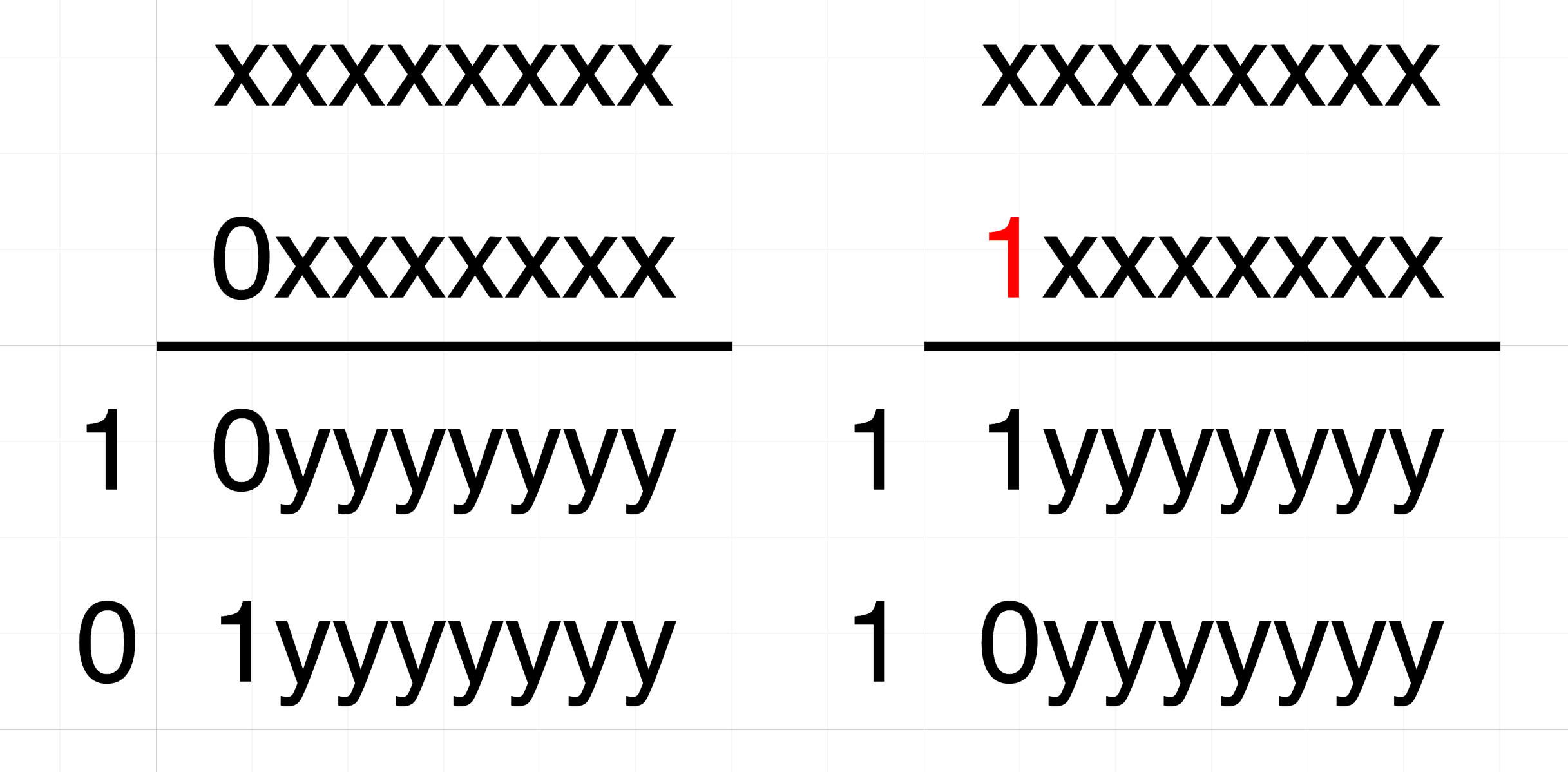
因此,0x80的差分值,在经过模256的加法后,肯定会导致加法的结果也有0x80的差分值。
解决完模256的加法后,再来看看循环左移:
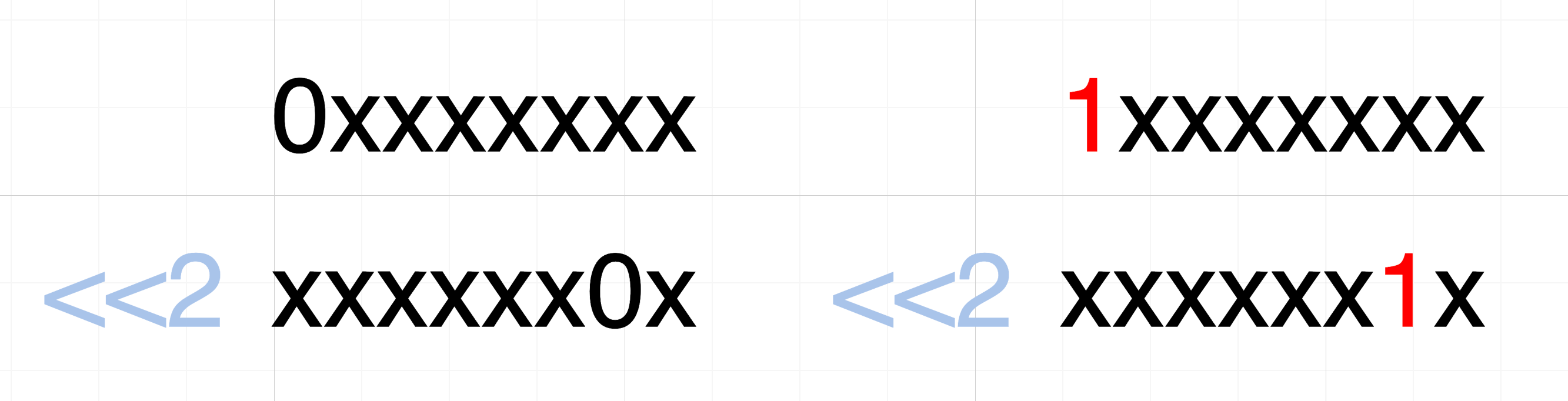
把差分值也同样循环右移了,0x80的差分值,在经过循环左移2bit后,差分值变为了0x02。
ok,这样我们就可以得到G函数的一个差分特征:G函数有多个输入,当其中一个输入的差分值为0x80,其他输入均相同(差分值为0x00)时,G函数输出的差分值为0x02。
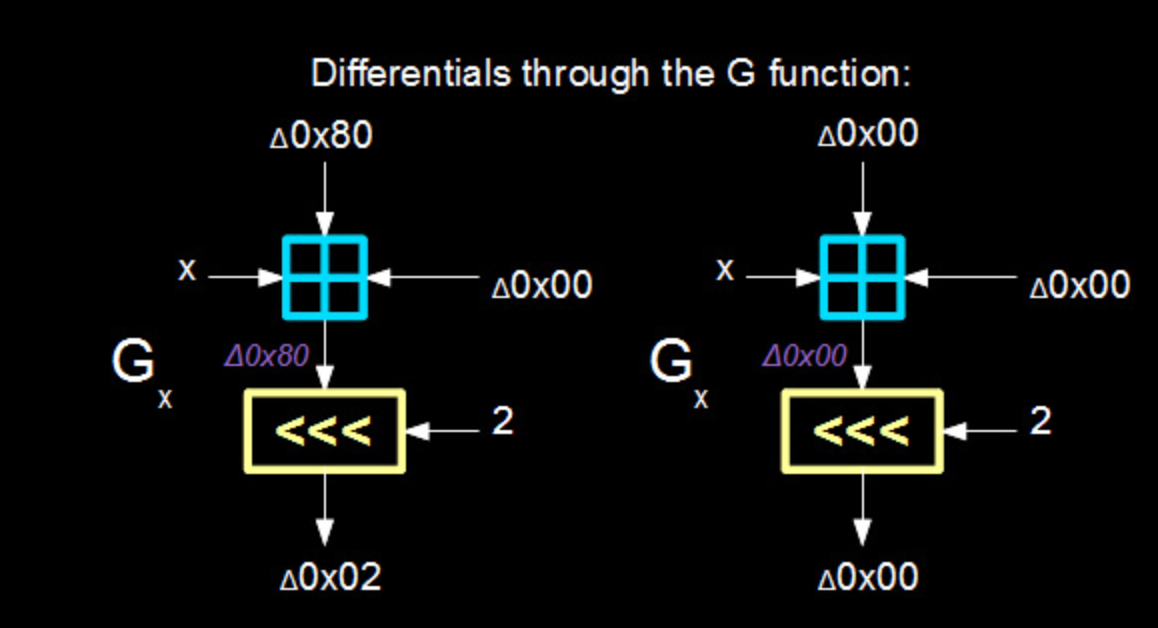
然后,再来看看外面的F函数:
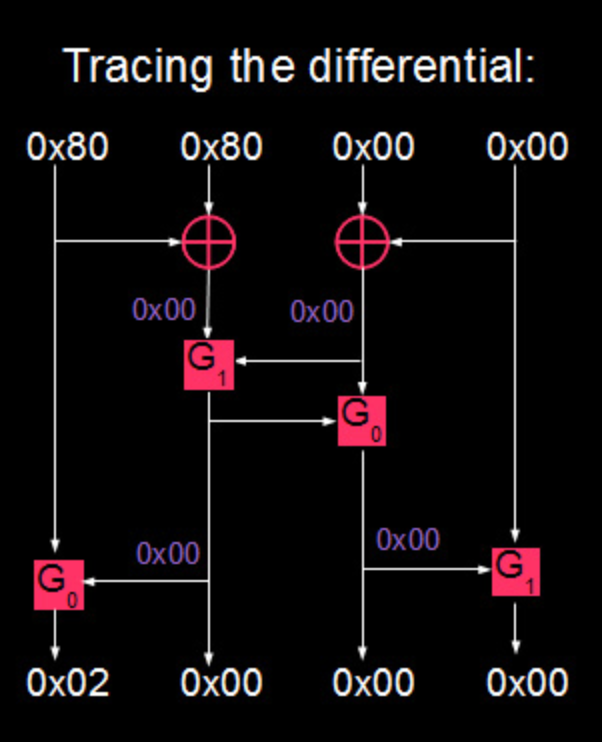
如图所示,输入0x80800000的差分值,将输出0x02000000的差分值。
这样,拿到F函数的一个差分值后,就可以对Feistel结构进行分析了:
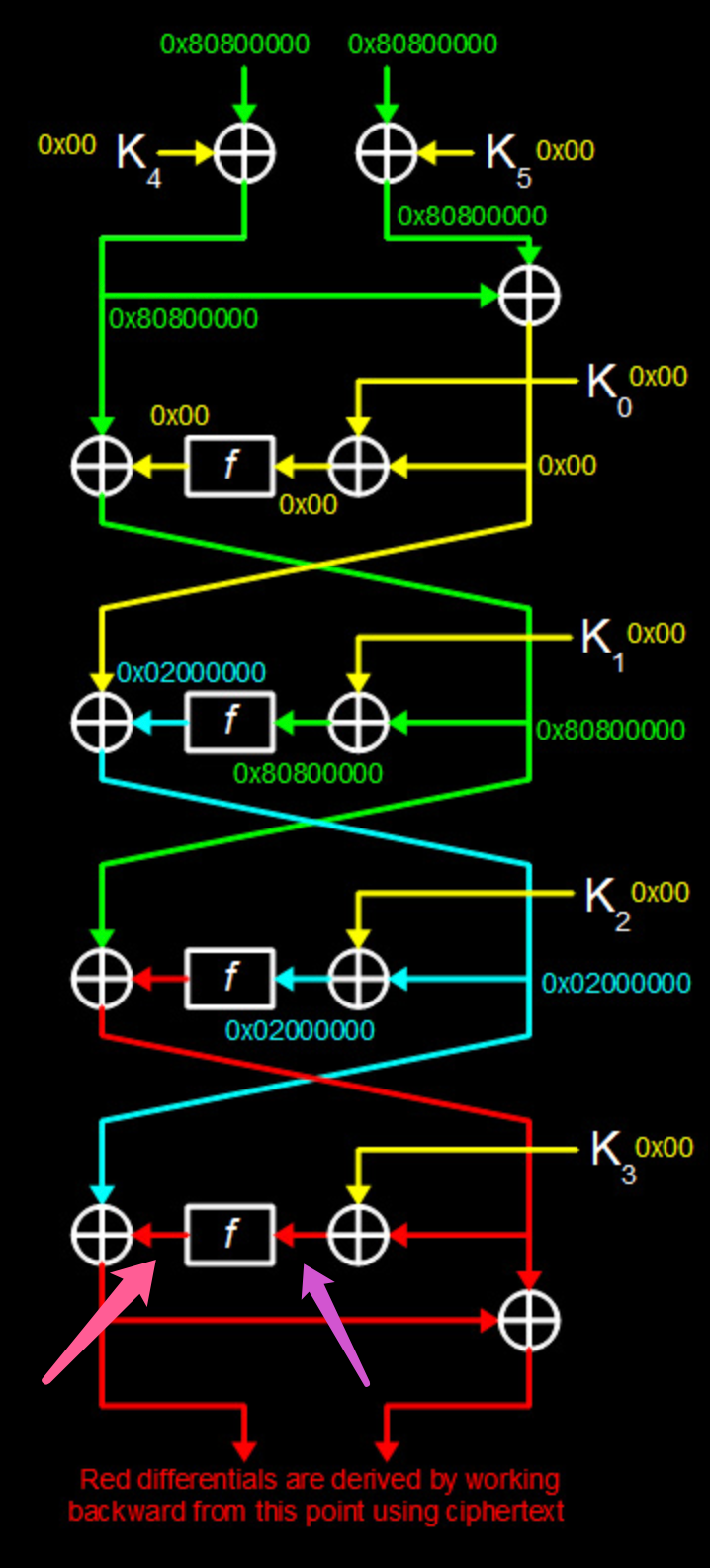
对明文输入0x80800000 80800000的差分值,将导致第4轮开始时L的差分值为0x02000000。
密文是已知的,可以从中反推到第4轮f函数输出的差分值(即下图紫色部分):L0 ^ L1 ^ 0x02000000
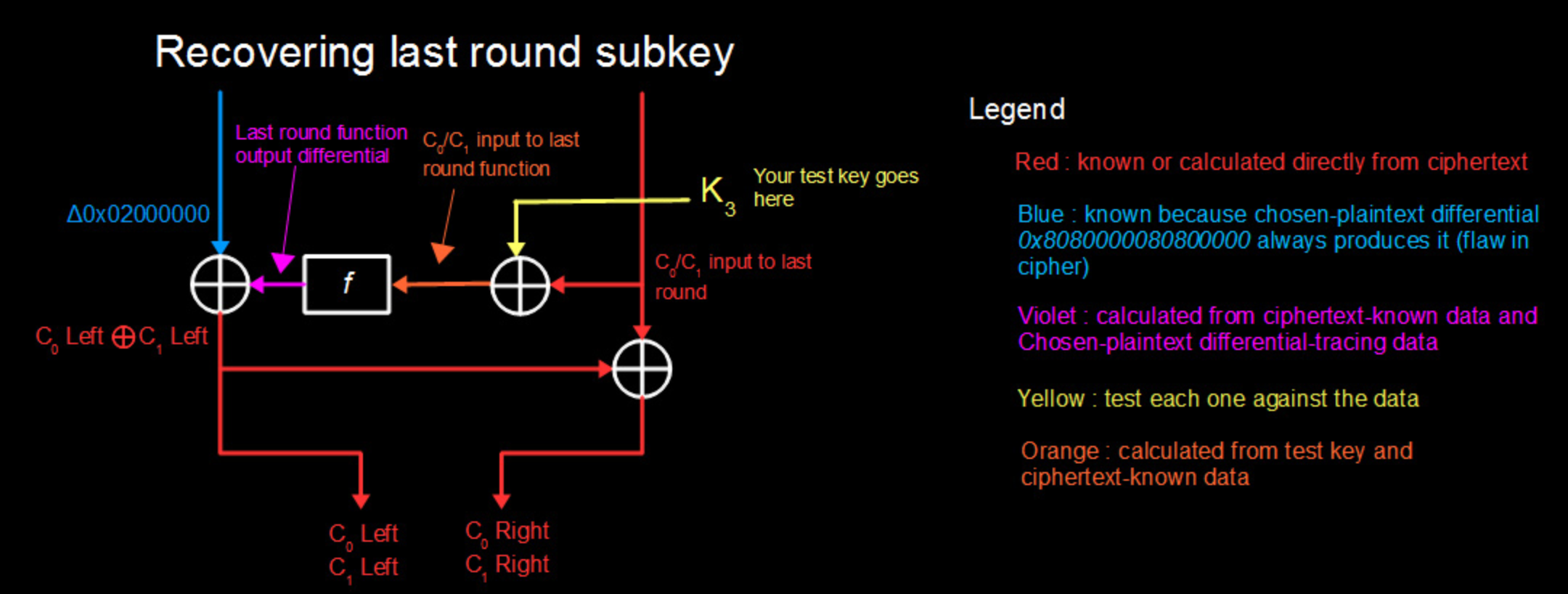
那么,如何日这第4轮的子密钥呢?
其实还是要枚举,但是可以通过差分攻击来将64-bit的key拆分成6个32-bit的round key,然后分别对这6个round key进行枚举,复杂度大幅降低。
对于已知的一对明密文(M0-C0, M1-C1),可以通过C0, C1反推到第四轮xor round key之前的R0, R1(上图右中)。可以对round key进行枚举,然后将R0 ^ K, R1 ^ K分别经过f函数,得到两个输出f(R0 ^ K), f(R1 ^ k),然后看这两个输出的差分值是否和L0 ^ L1 ^ 0x02000000相同。如果相同,那就说明这个round key很有可能就是真正的round key,可以将其记录下来,作为candidate keys。
再去找几对明密文,同样操作一下,可以将candidate keys的范围不断缩小,直至找到真正的round key。
事实上,round key不唯一。
6对明密文,大概率上可以得到4个可能的round key;
10对明密文,也能得到4个等价的round key;
20对明密文,也能得到4个等价的round key。
用这4个round key中的任何一个都可以解密。
先咕一下。。。