Intended Solution to Crypto Problems in WMCTF 2020

腾讯微云: https://share.weiyun.com/LH2u2wkm

MEGA: https://mega.nz/file/jT5TUYBQ#o6yjTM42yQViSl4djkuSwnqdmm0IGD3Mw4WHQq89-4U

Sum

Description

Special case of a NP-complete problem.

Flag

WMCTF{1508363197285327134921463070467158008637697619610562046}

Writeup

The subset-sum problem is proved to be NP-complete, which means, under the assumption $\mathcal{P} \ne \mathcal{NP}$, no polynomial time algorithm exists to solve it.

However, some special cases of the subset-sum problem have trivial solutions. For instance, the subset-sum problem of a super increasing sequence is quite easy to solve, which the Merkle-Hellman public key cryptosystem (invented in 1978) is based on. Unfortunately, Shamir broke the (original) Merkle-Hellman public key cryptosystem in 1982. Three years later, Lagarias and Odlyzko successfully reduced the subset-sum problem with low density to the shortest vector problem in lattice. Although SVP is proved to be NP-hard for randomized reductions by Ajtai, seemingly harder to handle, we have some powerful tools to solve it in low dimension——the lattice reduction algorithms!

In this challenge, we are given an instance of the subset-sum problem with low density ($d$ = 0.8). No doubt that this one belongs to the class that is easy to solve.

We are given a set of 180 elements $A = {a_0, a_1, \cdots, a_{179}}$, and a target number $s$, which is a sum of 160 of them.

To get the flag, we need to find a 0-1 vector $$ \mathbf{m} = {m_0, m_1, \cdots, m_{179}}, \quad m_i \in {0, 1} $$ such that $$ \sum_{i=0}^n {m_ia_i} = s. $$

For convenience, we reverse the “0"s and “1"s in the solution vector by calculating

$$ s’ = \sum_{i=0}^n {m_i} - s. $$

Then, the solution vector contains 20 “1"s and 160 “0"s.

From the special construction of this subset-sum instance, we can see that not only the density is small, the hamming weight (number of ‘1’s in the solution vector) is small as well.

One naive solution is to enumerate all the possible combinations and check whether the choice is correct. Ways of choosing 20 elements out of 180 amount to $$ {180\choose20} = 175142105857592248012292655 \approx 2^{88}. $$

This requires enormous computing power and seems to be infeasible in the current (2020).

However, it can be better solved by using lattice reduction. Since the hamming weight is fixed to be 160, we can construct a special lattice $\mathbf{L}$ generated by the following matrix: $$ \mathbf{B} = \begin{bmatrix} 1 & 0 & \cdots & 0 & Na_0 & N \newline 0 & 1 & \cdots & 0 & Na_1 & N \newline \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \newline 0 & 0 & \cdots & 1 & Na_{179} & N \newline 0 & 0 & \cdots & 0 & -Ns & -Nk \newline \end{bmatrix} $$ where $k$ is the hamming weight, and $N$ is a balance constant satisfying $N > \sqrt{n}$.

It’s easy to show that the row vector $\mathbf{m}^* = {m_0, m_1, \cdots, m_{179}, 0, 0}$ is a point on the lattice and the Euclidean norm of $\mathbf{m}^$ is quite small ($|\mathbf{m}^| = \sqrt{20}$). The shortest vector in the lattice $\mathbf{L}$ is likely to be $\mathbf{m}^$. Thus, we can try to find it by running lattice reduction algorithms. Note that if we randomly shuffle the row vectors of the lattice, lattice reduction algorithms will output different reduced results. So, we can keep trying to reduce different input row vectors until we find the shortest vector, i.e., the target vector $m^$.

Although this instance is an easy-to-solve one, the dimension is not that low——$n$ is 180. Simply continuously running the lattice reduction algorithms such as LLL, or BKZ could rarely success. We did algorithm performance test on lower dimensions. It took about several hours for a 140 dimension one to succeed, and as to 160 dimension, it cost 50+ hours. So, the running time of 180 dimension can be predicted as hundreds of hours.

Cleverly, we can reduce the dimension by forcing somewhere in $\mathbf{m}^*$ to be “0” and removing those from the lattice. In fact, this is a technique, called as “Zero-Forced Lattices”, originating from the NTRU technical report . The probability of (randomly) forcing a right coordination is ${160\choose1} / {180\choose1} = 8/9 \approx 0.8889$. And if want to force $r$ right coordinates, the probability is ${160\choose{r}}/{180\choose{r}}$. As can be seen from the following graph, the probability decreases exponentially as $r$ increases linearly.

This indicates that, by using the “Zero-Forced Lattices” technique, we can gain much in search efficiency due to the fact that the lattices have smaller dimensions, there is also great significance loss of efficiency due for that we need try many times to get a dimension-reduced lattice that contains the target vector. Therefore, using this technique does not optimize much, and sometimes may even need more computing power than not using this technique. Anyway, there must exist an optimal choice of $r$ to achieve the most optimization. However, it is a little bit difficult (or just because of laziness) to find such an optimal choice. Instead of doing some experiments to find the optimal choice, we choose $r$ to be 40.

On the other hand, since we need to keep running lattice reduction algorithms in order to search for the target vector, this procedure can be easily speeded up linearly by multicore computing. That is, assuming that it requires 100 CPU hours on average to find the target vector, we can run this algorithm on 100 CPUs, and just need about 1 hour.

For the purpose of testing, we rented 4 cloud virtual machine instances from the cloud service provider Tencent , where each instance was equipped with a 32-core CPU and 64GB RAM and only cost 0.8RMB/hour. And then we ran our algorithm to search for the target vector. We were quite lucky, it took just about 300+ CPU hours to find the solution:

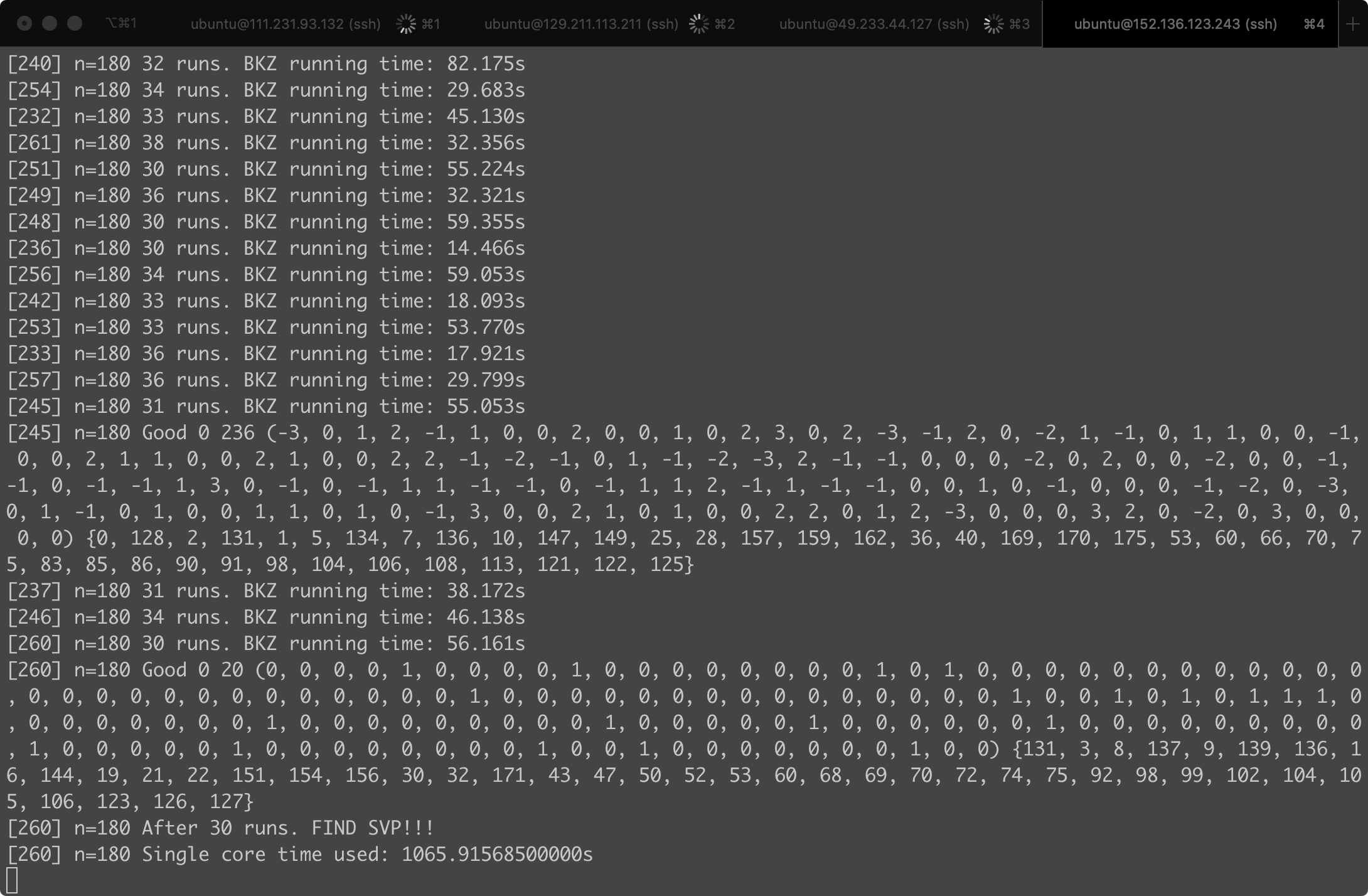
In fact, we had run in total 30000+ times of lattice reduction algorithms before we found this solution.

The source code is shown as below (written in SageMath 9.1):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95

# !/usr/bin/env sage
import random
import multiprocessing as mp

from json import load
from functools import partial


def check(sol, A, s):
    """Check whether *sol* is a solution to the subset-sum problem."""
    return sum(x*a for x, a in zip(sol, A)) == s


def solve(A, n, k, s, r, ID=None, BS=22):
    N = ceil(sqrt(n)) # parameter used in the construction of lattice
    rand = random.Random(x=ID) # seed

    indexes = set(range(n))
    small_vec = None

    itr = 0
    total_time = 0.0
    while True:
        # 1. initalization
        t0 = cputime()
        itr += 1
        # print(f"[{ID}] n={n} Start... {itr}")

        # 2. Zero Force
        kick_out = set(sample(range(n), r))
        # (k+1) * (k+2)
        # 1 0 ... 0 a0*N   N
        # 0 1 ... 0 a1*N   N
        # . . ... . ...    .
        # 0 0 ... 1 a_k*N N
        # 0 0 ... 0 s*N    k*N
        new_set = [A[i] for i in indexes - kick_out]
        lat = []
        for i,a in enumerate(new_set):
            lat.append([1*(j==i) for j in range(n-r)] + [N*a] + [N])
        lat.append([0]*(n-r) + [N*s] + [k*N])

        # 3. Randomly shuffle
        shuffle(lat, random=rand.random)

        # 4. BKZ!!!
        m = matrix(ZZ, lat)
        t_BKZ = cputime()
        m_BKZ = m.BKZ(block_size=BS)
        print(f"[{ID}] n={n} {itr} runs. BKZ running time: {cputime(t_BKZ):.3f}s")

        # 5. Check the result
        # print(f"[{ID}] n={n} first vector norm: {m_BKZ[0].norm().n(digits=4)}")
        for i, row in enumerate(m_BKZ):
            if check(row, new_set, s) and row.norm()^2 < 300:
                if small_vec == None:
                    small_vec = row
                elif small_vec.norm() > row.norm():
                    small_vec = row
                    print(f"[{ID}] n={n} Good", i, row.norm()^2, row, kick_out)
                    if row.norm()^2 == k:
                        print(f"[{ID}] n={n} After {itr} runs. FIND SVP!!!\n"
                              f"[{ID}] n={n} Single core time used: {total_time}s")
                        return True

        # 6. log average time per iteration
        itr_time = cputime(t0)
        total_time += itr_time
        # average_time = float(total_time / itr)
        # print(f"[{ID}] n={n} average time per itr: {average_time:.3f}s")



def main():
    CPU_CORE_NUM = 32

    k, n, d = 160, 180, 0.8
    s, A = load(open("data", "r"))
    r = 40 # ZERO FORCE

    new_k = n - k
    new_s = sum(A) - s
    solve_n = partial(solve, A, n, new_k, new_s, r)
    with mp.Pool(CPU_CORE_NUM) as pool:
        reslist = pool.imap_unordered(solve_n, range(200, 200+CPU_CORE_NUM))

        # terminate all processes once one process returns
        for res in reslist:
            if res:
                pool.terminate()
                break


if __name__ == "__main__":
    main()

PS: The BKZ algorithm in SageMath is underlying using the implementation of fplll . Since most of the time of the program is spent on running the BKZ algorithm, there is little performance loss by using SageMath, which is based on Python.

babySum

Description

Easy instance of the special case of a NP-complete problem.

Flag

WMCTF{83077532752999414286785898029842440}

Writeup

Same as the challenge Sum except for lower dimension.

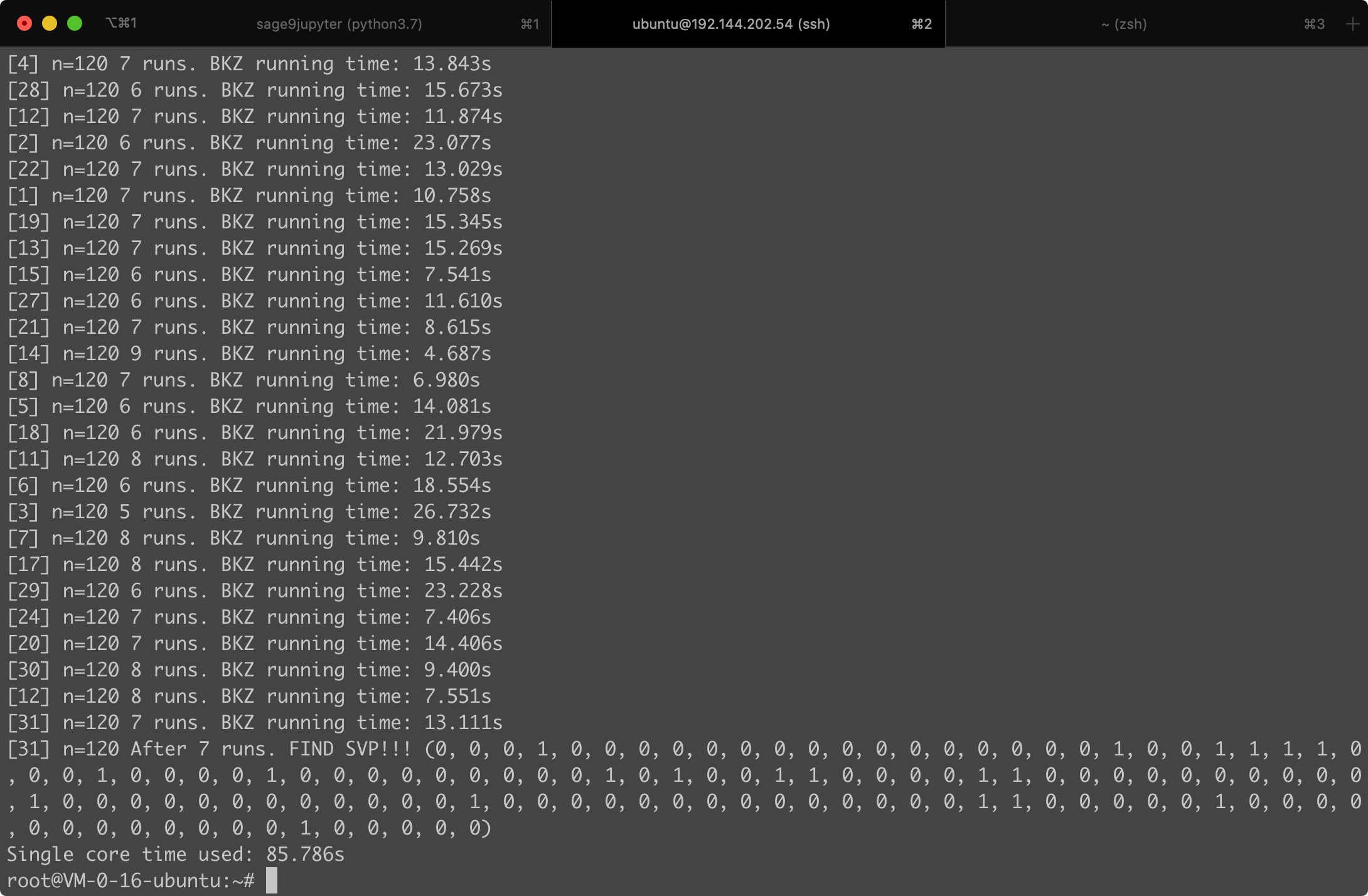
Game

Description

An arrogant prince is cursed to live as a terrifying beast until he finds true love.

Flag

WMCTF{Dont_ever_tell_anybody_anything___If_you_do__you_start_missing_everybody}

Writeup

This challenge is an instance of BEAST (Browser Exploit Against SSL/TLS) attack. This is a real world attack that was used to exploit against SSL 3.0/TLS 1.0 protocol and had prompted the movement to TLS 1.1.

Regarding more information about the attack, we refer to the following resources:

• How the BEAST Attack Works | Netsparker
• Origin Paper: Here Come The ⊕ Ninjas

In this challenge, A simulation of the security game as described in the paper is implemented with some modification. To get the flag, we need to guess a secret 48 random bytes. The only useful function the server provided is encrypting the secret prepended by something the client gives by using AES-CBC.

CBC mode is one of the most popular block cipher modes of operations. It can be shown as below:

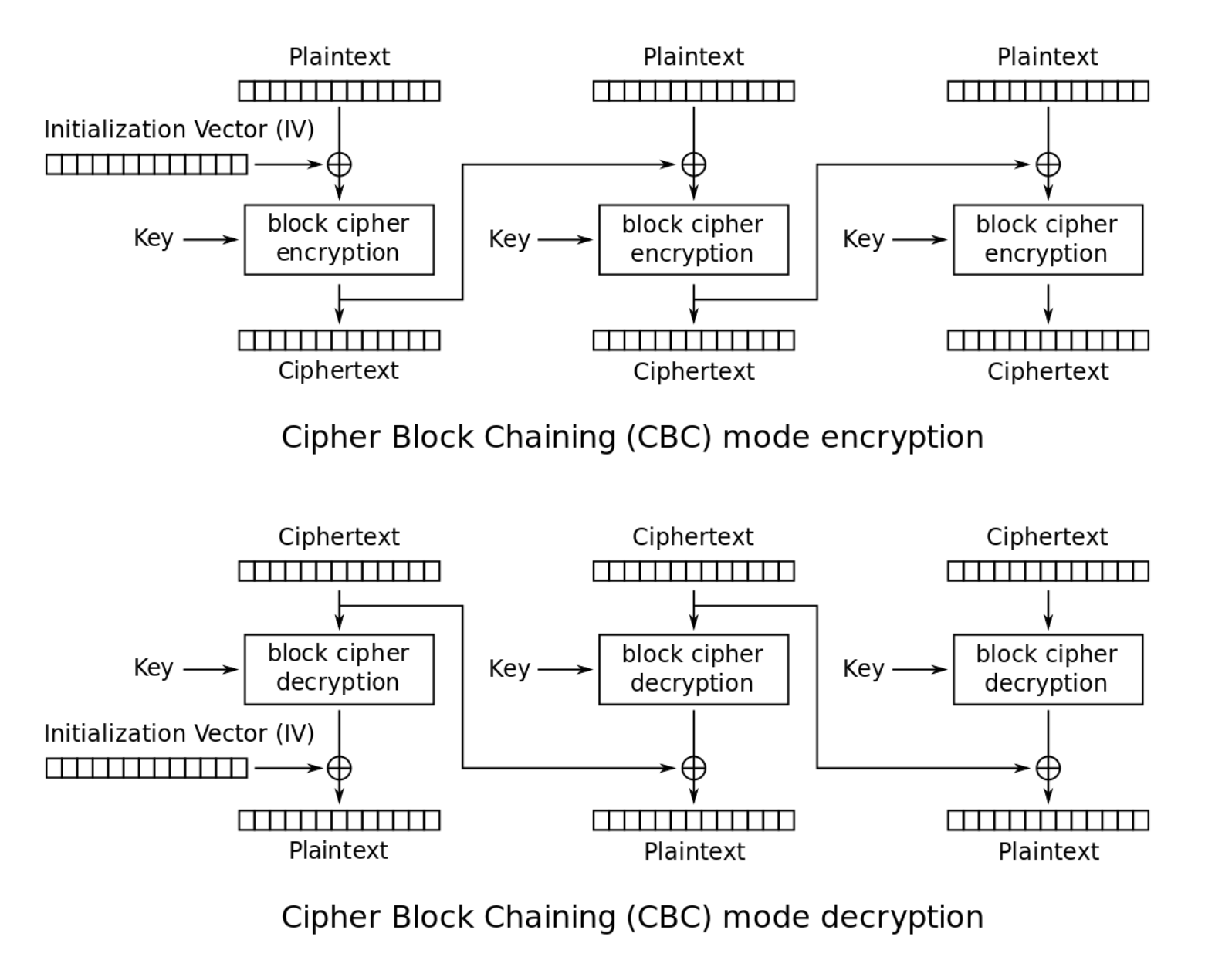
(picture from wiki )

The fatal vulnerability in this challenge is that, the initialization vector (IV) can be predicted during each encryption. This gives us space to manipulate the input of the block cipher encryption. Along with the (strange) encryption function the server provided, we can amout a chosen plaintext attack to recover the secret bytes.

We can consider the block cipher encryption as a pseudorandom permutation (PRP) that randomly permutes the input 16 bytes to another 16 bytes. The permutation depends only on the key and the same input results in the same output. So, if we are given a ciphertext (16 bytes), we can try all the possible input to the block cipher encryption until the output is the ciphertext. No doubt that this is infeasible because the size of plaintext space is $256^{16}$. However, if we have knownledge of the first 15 bytes of the input, it’s easy to recover the last unkown byte by bruteforcing all the possible choices (only 256) of the last bytes, and check whether the output is the corresponding ciphertext.

We mean block cipher encryption as AES encryption using ECB mode with one block.

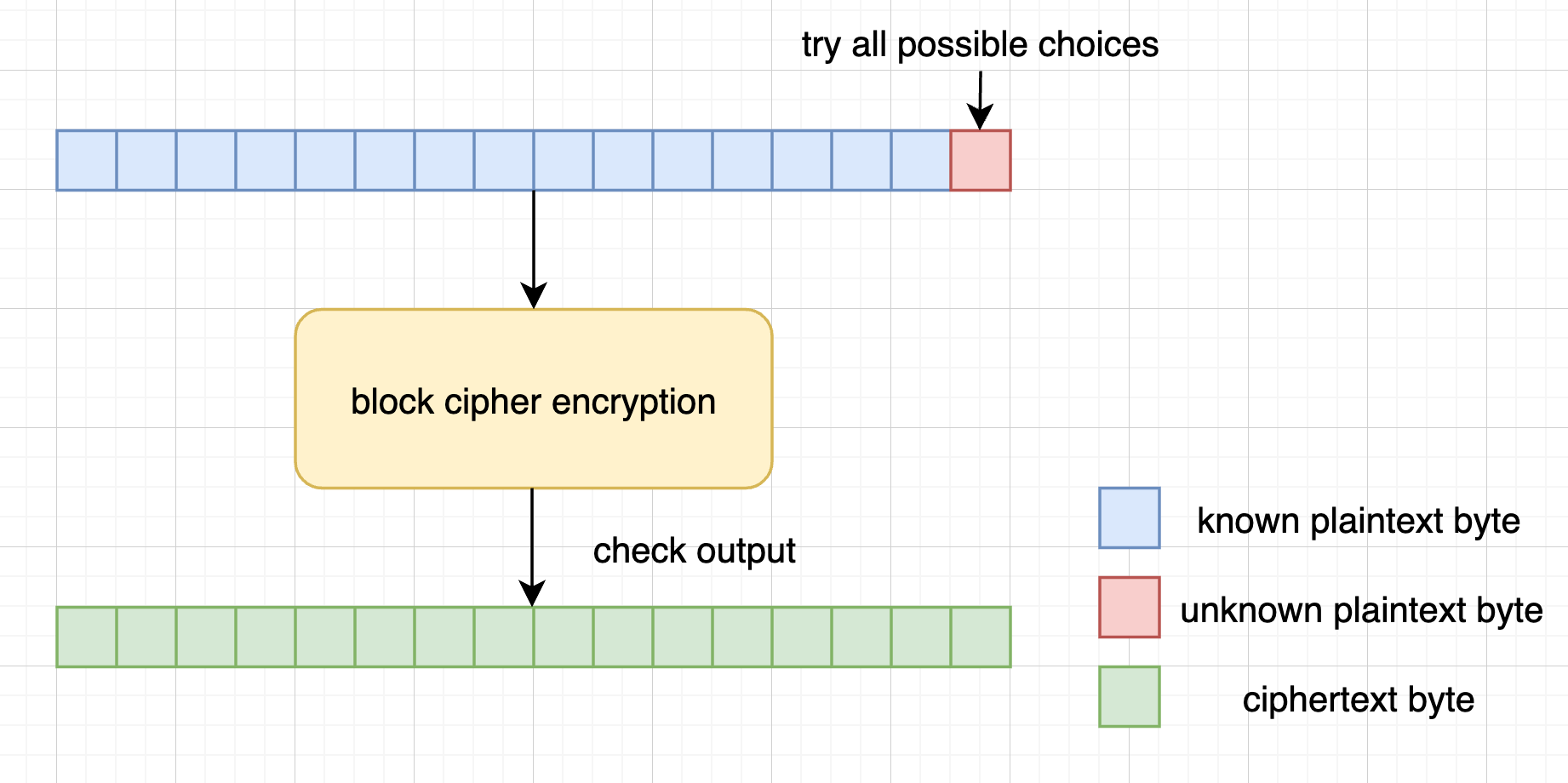
(How to recover the last byte)

Back to this instance, the chosen plaintext attack consists of two phases:

1. Get the ciphertext of 15 known plaintext bytes and 1 unknown byte that we want to recover.
2. Try all the possible choices of the last unknown byte until the output is exactly the ciphertext, thus recovering the last byte.

But, this arises two questions as well:

1. How can we control the input of the block cipher encryption?
2. How come we are aware of the 15 plaintext bytes?

For the first one, we can find that the IV of each encryption is predictable. Strictly, IV should only stand for the first xor vector before block cipher encryption. Here, however, we mean IV by all the xor vectors. The first IV is provided by the server and later ones are the ciphertexts of previous block. To control the input of the block cipher encryption, we can send the server a payload that has been xored with the predicted IV. For example, if we want the input of block cipher encryption to be $P$, and the predicted IV is $iv$, we can send the payload as $P \oplus iv$.

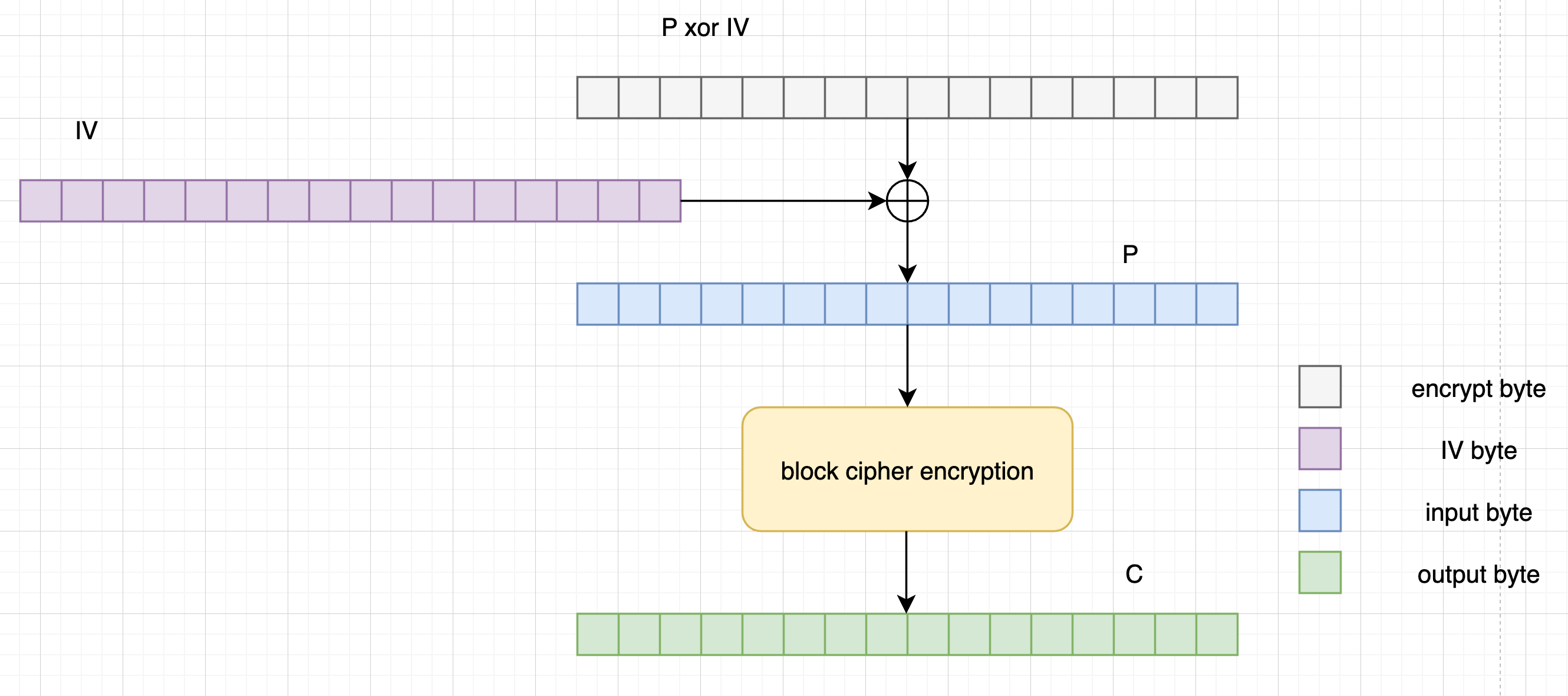
(How to control the input of the block cipher encryption)

As to the second one, since the server receives anything the client sends, we can control the block boundary by prepending well-prepared amounts of bytes. For example, if we send 15 bytes $B$ to the server, the server will encrypt $B\ || \ \text{secert}$. This will be grouped into $[B\ ||\ \text{secret}0], [\text{secret}{1-16}], [\text{secret}{17-32}], [\text{secret}{33-47}\ ||\ \text{pad}]$, and then xor with the corresponding IV to do the block cipher encryption. Therefore, the first block indeed satisfies the condition.

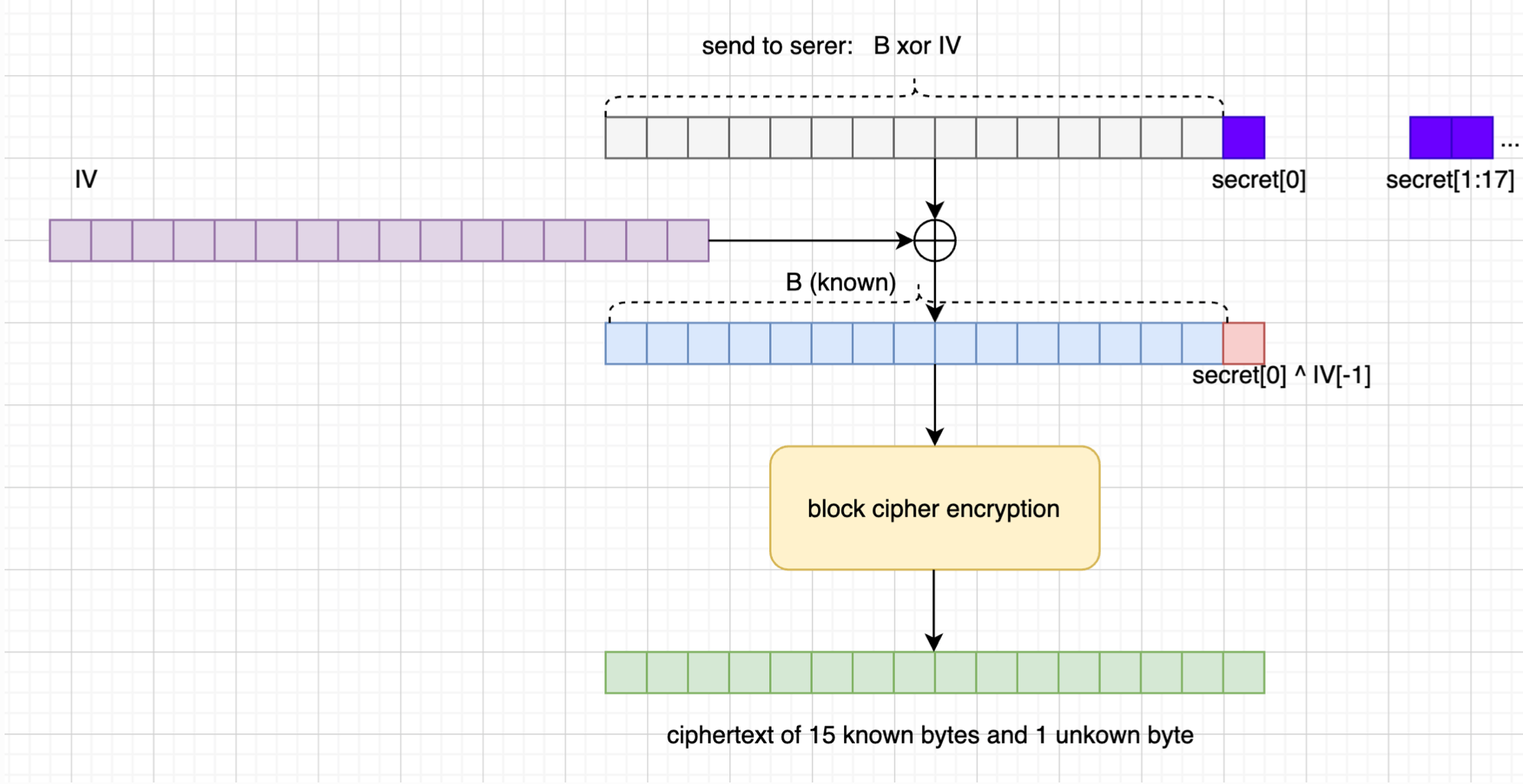
(How to get the ciphertext of 15 known plaintext bytes)

After we have successfully recovered the first byte of the secret, we can consider the recovered as known bytes and send 14 bytes to the server to try recovering the second secret byte. By repeating this attack 48 times, we can recover all the 48 bytes of the secret and then go to get the 🚩. On average, it requires about $128 \times 48 = 6144$ quries. We set the alarm time as 1200 seconds (20 minutes). It’s sufficient to complete the exploit. 🤔

The source code of the exploit is provided as below (written in Python 3.8):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89

# !/usr/bin/env python3
import re, string
from hashlib import sha256
from itertools import product

from pwn import *

def xor(a, b):
    return bytes(x^y for x, y in zip(a, b))

def hex2bytes(data):
    return bytes.fromhex(data.decode())


r = remote("127.0.0.1", 10000)
# context.log_level = 'debug'

# PoW
r.recvlines(13) # banner
rec = r.recvline().decode()
suffix = re.findall(r'XXXX\+([^\)]+)', rec)[0]
digest = re.findall(r'== ([^\n]+)', rec)[0]
print(f"suffix: {suffix} \ndigest: {digest}")
print('Calculating hash...')
for i in product(string.ascii_letters + string.digits, repeat=4):
    prefix = ''.join(i)
    guess = prefix + suffix
    if sha256(guess.encode()).hexdigest() == digest:
        print(guess)
        break
r.sendafter(b'Give me XXXX: ', prefix.encode())

# Attack
rec = r.recvline().decode()
IV_hex = re.findall(r'([0-9a-f]{32})', rec)[0]
IV = bytes.fromhex(IV_hex)

def getLastBit(known, cipher, IV):
    """
    known: first 15 bytes that we know

    cipher: Ek(known + ?) where ? is one byte that we want to get

    returns (?, IV)
    """
    for i in range(256):
        r.sendlineafter(b"> ", b"1")
        payload = xor(IV, known + bytes([i]))  # Ek(known + i) where len(known) = 15, len(i) = 1
        r.sendlineafter(b"(in hex): ", payload.hex().encode())

        rec = r.recvline(keepends=False)
        IV = hex2bytes(rec[-16*2:])
        if hex2bytes(rec[:16*2]) == cipher:
            return bytes([i]), IV
    return None

# Recover byte by byte.
recovered = b""
for k in range(4):
    # k=0: secret[0:15]   l={15, 14, ..., 1}
    # k=1: secret[15:31]  l={16, 15, ..., 1}
    # k=2: secret[31:47]  l={16, 15, ..., 1}
    # k=3: secret[47:48]  l={16}
    start = 15 if k == 0 else 16
    end   = 15 if k == 3 else 0
    for l in range(start, end, -1):
        r.sendlineafter(b"> ", b"1")
        r.sendlineafter(b"(in hex): ", IV[:l].hex().encode())
        rec = hex2bytes(r.recvline(keepends=False))
        if k == 0:
            known = b"\x00"*l + xor(IV[l:-1], recovered)
            last_byte = IV[-1:]
            cipher, IV = rec[:16], rec[-16:]
        else:
            known_IV, cipher, IV = rec[16*(k-1):16*k], rec[16*k:16*(k+1)], rec[-16:]
            known = xor(known_IV, recovered[-15:])
            last_byte = known_IV[-1:]

        byte, IV = getLastBit(known, cipher, IV)
        recovered += xor(byte, last_byte)
        print(recovered.hex(), len(recovered))

# Get flag.
r.sendlineafter(b"> ", b"2")
r.sendlineafter(b"(in hex): ", recovered.hex().encode())
print(r.recvline(keepends=False))
# b'TQL!!! Here is your flag: WMCTF{Dont_ever_tell_anybody_anything___If_you_do__you_start_missing_everybody}'

r.close()