Writeup for Crypto Problems in HufuCTF 2020

GM

makekey函数中，有

$$ \begin{aligned} (q^2 x)^\frac{p-1}{2} &\equiv q^{p-1} x^\frac{p-1}{2} \equiv (\frac{x}{p})\pmod{p} \newline (p^2 x)^\frac{q-1}{2} &\equiv p^{q-1} x^\frac{q-1}{2} \equiv (\frac{x}{q})\pmod{q} \end{aligned} $$

其中，$(\frac{x}{p})\pmod{p}$表示$x$在$F_p$下的勒让德符号。

要满足

$$ (q^2 x)^\frac{p-1}{2} + (p^2 x)^\frac{q-1}{2} = n - phi - 1 = pq - (pq - p - q + 1) - 1 = (p-1) + (q-1) $$

只有 $$ \begin{aligned} (q^2 x)^\frac{p-1}{2} &= p-1 \equiv -1 \pmod{p} \newline (p^2 x)^\frac{q-1}{2} &= q-1 \equiv -1 \pmod{q} \end{aligned} $$

也就是说$x$是在$F_p, F_q$下的二次非剩余（Quadratic Nonresidue）。

加密过程则是对msg的每一bit进行加密： $$ c \equiv x^{br || bi} \cdot r^2 \pmod{N} $$ br是一个随机数$r$的二进制表示，bi是msg的某一bit（0或1）。

也就相当于 $$ c \equiv x^{2r + bi} \cdot r^2 \pmod{N} $$

我们可以来考察这个$c$在$F_p, F_q$下的勒让德符号： $$ \begin{aligned} (\frac{c}{p}) \equiv (\frac{x^{2r} x^{bi} r^2 }{p}) \equiv (\frac{x^r}{p})^2 (\frac{x^{bi}}{p}) (\frac{r}{p})^2 \equiv (\frac{x^{bi}}{p}) \pmod{p} \newline (\frac{c}{q}) \equiv (\frac{x^{2r} x^{bi} r^2 }{q}) \equiv (\frac{x^r}{q})^2 (\frac{x^{bi}}{q}) (\frac{r}{q})^2 \equiv (\frac{x^{bi}}{q}) \pmod{q} \end{aligned} $$

msg的这一位bi是0的话，两个勒让德符号肯定都是1；如果这一位bi是1的话，勒让德符号肯定都是-1（p-1或q-1）。

因此可以通过勒让德符号推算出bi，进而得到msg。

给了n和phi，直接利用sagemath的解方程功能就可以拿到p, q。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


# sage 8.9
N   = 9433451661749413225919414595243321311762902037908850954799703396083863718641136503053215995576558003171249192969972864840795298784730553210417983714593764557582927434784915177639731998310891168685999240937407871771369971713515313634198744616074610866924094854671900334810353127446778607137157751925680243990905528141072864168544519279897224494849206184262202130305820187569148057247731243651084258194009459936702909655448969693589800987266378249891157940262898554047247605049549997783511107373248462587318323152524969684724690316918761387154882496367769626921299091688377118938693074486325995308403232228282839975697
phi = 9433451661749413225919414595243321311762902037908850954799703396083863718641136503053215995576558003171249192969972864840795298784730553210417983714593764557582927434784915177639731998310891168685999240937407871771369971713515313634198744616074610866924094854671900334810353127446778607137157751925680243990711180904598841255660443214091848674376245163953774717113246203928244509033734184913005865837620134831142880711832256634797590773413831659733615722574830257496801417760337073484838170554497953033487131634973371143357507027731899402777169516770264218656483487045393156894832885628843858316679793205572348688820

var("p q")
print solve([p*q == N, p*q - p - q + 1 == phi], p, q)
# [
# [p == 94130524494940356506875940901901506872984699033610928814269310978003376307730580667234209640309443564560267414630644861712331559440658853201804556781784493376284446426393074882942957446869925558422146677774085449915333876201669456003375126689843738090285370245240893337253184644114745083294361228182569510971, q == 100216711979082556377200124903474313599976321274816484378304672662900171906266478070844182716079881540999761528986068197079878654411887736955737660906283803174161740862819849415729979371880583995409044839777513091451849412985192528374337852907661670174530234397743068706607004213367391908429077794527921775907],
# [p == 100216711979082556377200124903474313599976321274816484378304672662900171906266478070844182716079881540999761528986068197079878654411887736955737660906283803174161740862819849415729979371880583995409044839777513091451849412985192528374337852907661670174530234397743068706607004213367391908429077794527921775907, q == 94130524494940356506875940901901506872984699033610928814269310978003376307730580667234209640309443564560267414630644861712331559440658853201804556781784493376284446426393074882942957446869925558422146677774085449915333876201669456003375126689843738090285370245240893337253184644114745083294361228182569510971]
# ]

可以直接求出p，q。

接下来只需要判断每一个c的勒让德符号（欧拉判别法）就可以知道msg的那一位是0还是1了。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


# python3
from Crypto.Util.number import long_to_bytes

p = ...
q = ...

def legendre(a, p):
    return pow(a, (p-1)//2, p)

ciphers = open("output", "r").readlines()[2]
ciphers = [int(c)  for c in ciphers[1:-3].replace("L", "").split(", ")]

msg = ""
for c in ciphers:
    lp = legendre(c, p)
    lq = legendre(c, q)
    if lp == 1 and lq == 1:
        msg += "0"
    else:
        msg += "1"

print(long_to_bytes(int(msg, 2)))
# flag{bd4f1790-f4a2-4904-b4d2-8db8b24fd864}

mceliece

这题比赛结束后的1个半小时，才做出来，总算意识到我是多么菜了。。

没见过这玩意，得现学。。

网上搜了下，直接搜mceliece就能搜到，但是，woc？什么玩意儿？？？

搜了很多资料，但是都没怎么看得进去。。

有些paper，是建立在你对这个东西已经有一定了解的基础上的。。直接一上来就看，体验的确很差。

也搜到了hack.lu 2017的一道同名题（但是只能找到一个exp）：

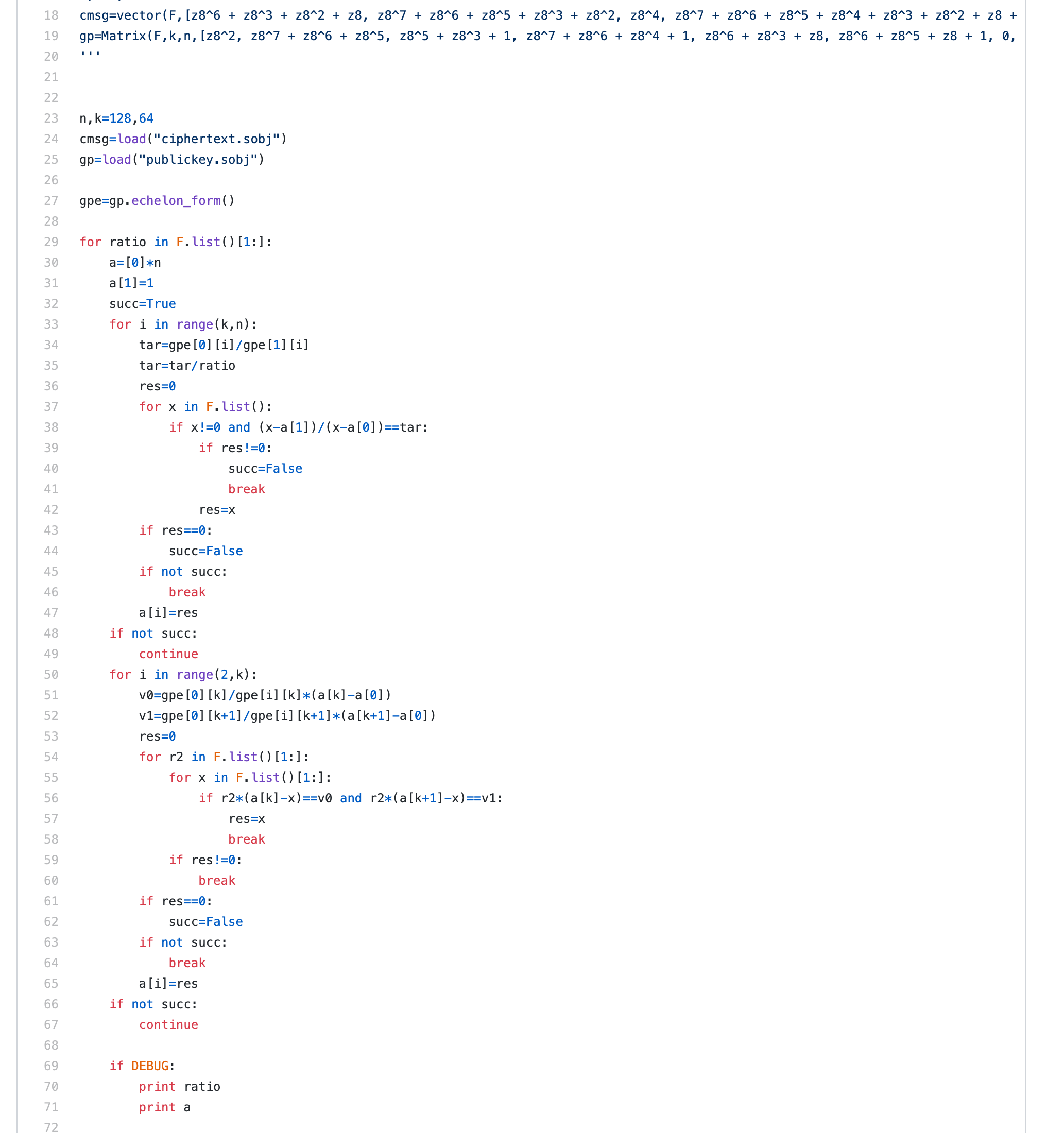
Screen Shot 2020-04-19 at 9.04.31 PM

这个代码，tmd，写得也太烂了吧。。

而且还没题目具体内容，不能抄一波作业。。很难受

后来找到了一篇比较好上手的资料： https://arxiv.org/pdf/1907.12754.pdf

前面两章没怎么仔细看（因为看不太懂。。），直接去看了点第3章。

实际上，这个Mceliece跟GGH很相似。

都是明文msg乘上一个矩阵，线性变换一波，然后加上一点error，让别人很难去解密，只有掌握了trapdoor information的才能去解密。

不同于GGH的解密是利用lattice的good basis, bad basis, Babai's algorithm，这里的解密是利用了纠错码的作用，能够对增添了error的内容进行纠错，得到没有被误扰的结果，然后乘一下逆矩阵就能搞回msg了。

给的pubkey是$G’ = S\cdot G\cdot P$，其中$S$是一个k × k = 28 × 28 的矩阵，$G$是一个k × n = 28 × 64的矩阵，$P$是一个n × n = 64 × 64的矩阵，所以$G’$是一个k × n = 28 × 64的矩阵。

对明文进行了一个分组，每组64bits，进行加密： $$ c = m \cdot G’ + e $$ 更详细的操作过程：

Screen Shot 2020-04-19 at 9.15.11 PM

这一题的Mceliece cryptosystem的问题就出现在他给的参数很小：$n = 2^6 = 64, k = 28, t = 6$

但是直接去爆破的话，找不准要爆的那个目标是很难搞的。

我一开始就想着能不能遍历他所有一开始生成这个crypto = McElieceCryptosystem(n,m,irr_poly);中的irr_poly，不过短暂的分析后，显然是不太现实的：

irr_poly的系数是$GF(2^6)$上的元素，总共有64个，irr_poly是一个多项式，最高次数为6，所以一共有$64^7 = 2^{42}$种可能，虽然有irreducible这个条件，但还是很多。。而且sage的运行速度挺慢的。

那么应该去日他的哪里呢？

那就需要继续看下去：

Screen Shot 2020-04-19 at 9.20.59 PM

噢，原来Mceliece的e跟GGH的e差不多啊。。都是被日的突破口（GGH的Nguyen Attack也是从这个e入手的）

上面图片的意思就是说，如果参数太小了的话，这个纠错码的纠错能力t就会很小，然后e（一个1 × n = 1 × 64 的向量）里面最多有t个地方能够取值为1，其他地方必须取值0，否则加密之后就不能纠错回来了。

那么这一题的t = 6，从64里面选6个地方，$C_{42}^6 = 74974368$，也就七千多万种可能，能爆。。。

不过又有很难受的一点就是，他的每一组加密的时候，e是随机取的，也就是说每一组所对应的e是不一样的，而且一共有13组加密。。

不过，如果我们继续再看下去，会发现资料里给了一个算法：Lee-Brickell algorithm：

Screen Shot 2020-04-19 at 9.30.31 PM

我们可以尝试着去实现一下这个算法，这样我们就可以直接利用这个算法去找到每一组所对应的e。

不过，这上面写的也挺难理解的。。

首先，什么是information set？？？

找了一会，终于在上面的19页中间部分找到了他的定义：

Screen Shot 2020-04-19 at 9.33.04 PM

也就是抽取$G$（用来编码的generator matrix）的若干列，且抽出来新生成的k × k = 28 × 28矩阵必须得是可逆的。

回到这个算法里，他又冒出来一个参数p？？？？无法理解是怎么取的。。

但是看到算法的step 3的时候，我大概了解到了这个p是多少了。

我们这一题的矩阵是在GF(2)上的，然后step 3里面说for each x1, x2, . . . , xp ∈ Fq \ {0}，也就是x ∈ GF(2) \ {0} = {1}，那么xp只有1个，所以p = 1。

其实在实现这个算法到step 3的时候，我就不知道怎么继续下去了，然后去google了一个Lee-Brickell algorithm，发现SageMath里面居然是自带这种编码的函数的，而且已经实现好了这个算法！！！SageMath果然神器啊。

http://doc.sagemath.org/html/en/reference/coding/sage/coding/information_set_decoder.html

Screen Shot 2020-04-19 at 9.40.20 PM

于是就找到了SageMath相应的源码位置，发现官方实现和我的代码居然有那么一些的神似：

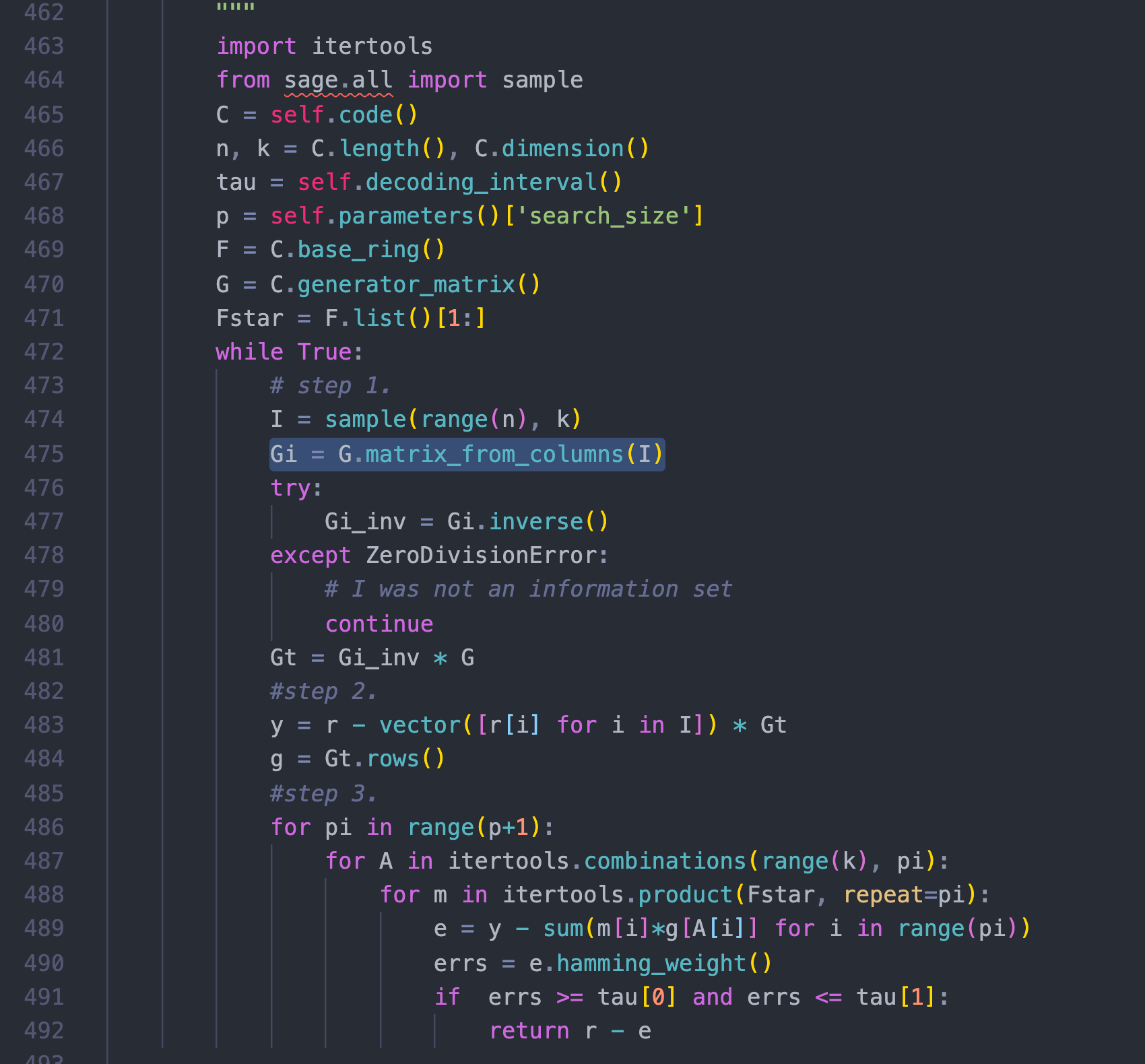
Screen Shot 2020-04-19 at 5.43.15 PM

⬆️官方实现 ⬇️我的实现

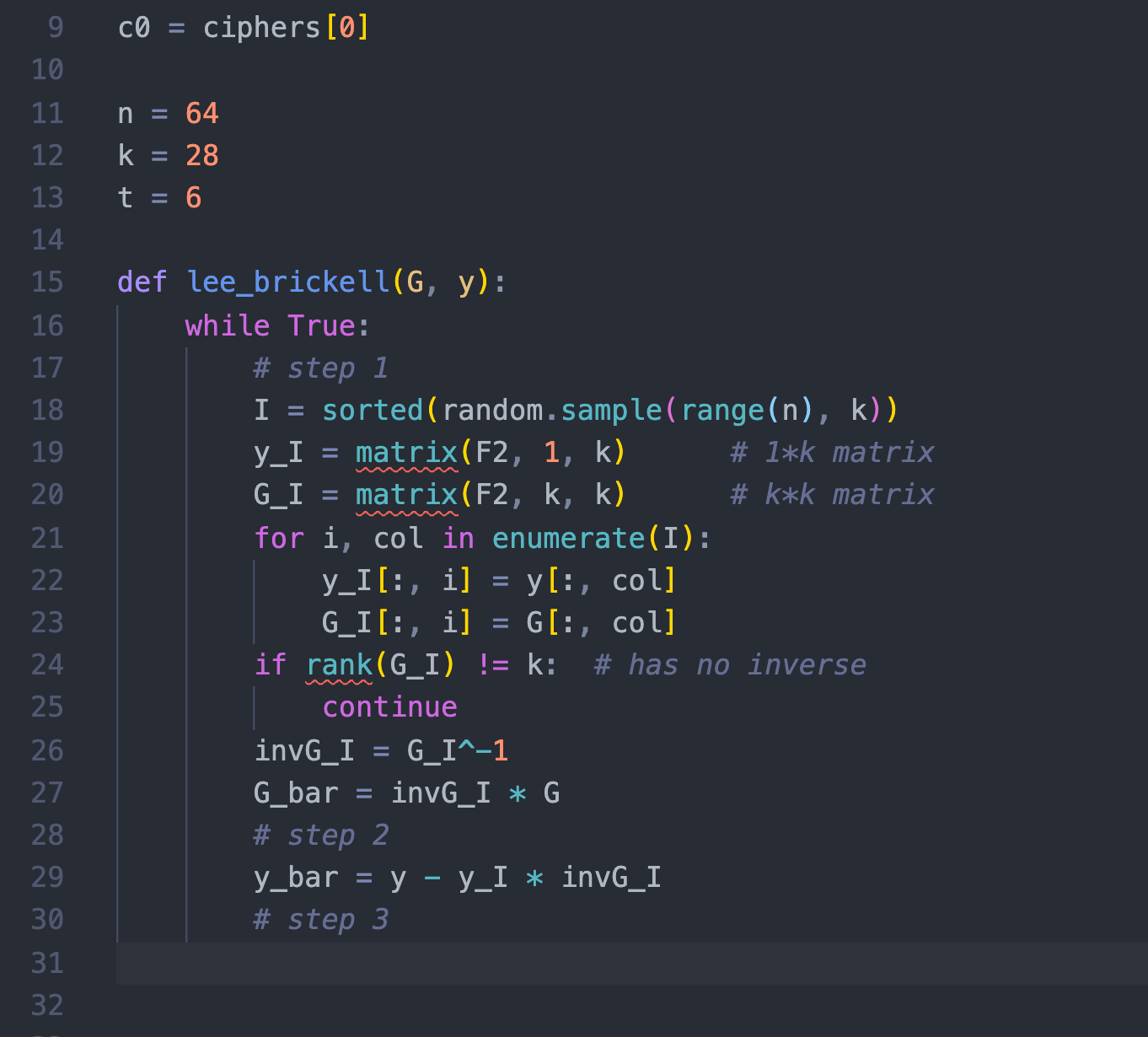
Screen Shot 2020-04-19 at 5.43.06 PM

本来想直接用官方给的函数的，但是运行会报错（后来才发现原来是因为需要vector类型的c0，而非matrix类型的c0，因为load出来的c0 = ciphers[0]，是matrix类型的，需要取他的第一行c0[0]得到vector类型，再A.decode(c0[0])才行。。真的是太坑了！！！不，应该是我太菜了，不是那么地熟悉SageMath）：

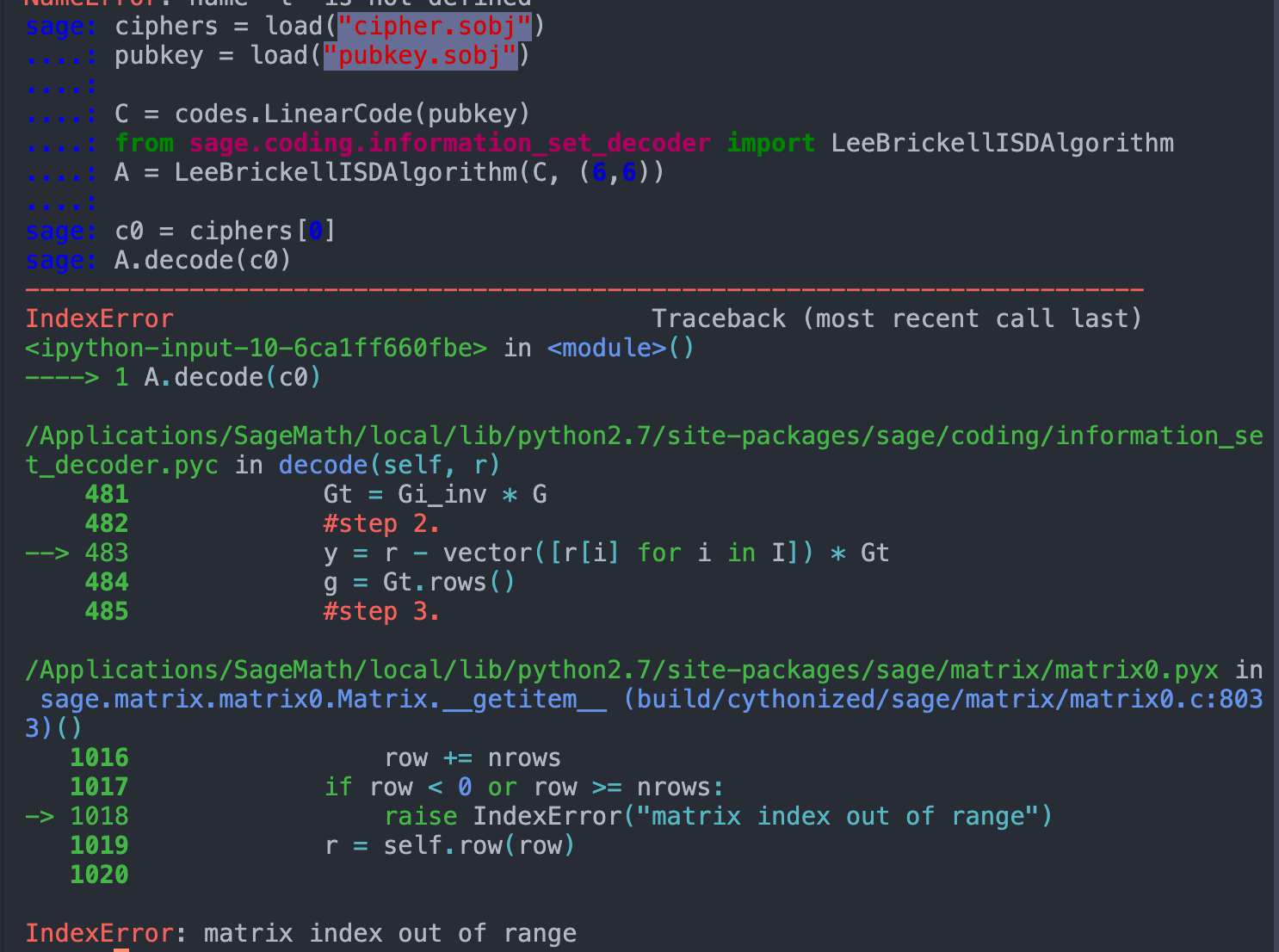
Screen Shot 2020-04-19 at 9.44.00 PM

然后，我就对比着官方实现，写好了我自己的实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


# sage 8.9
ciphers = load("cipher.sobj")
pubkey = load("pubkey.sobj")

n = 64
k = 28
t = 6
F2 = GF(2)
def GetRowVectorWeight(n):
    return sum(ZZ(i) for i in n[0])

def lee_brickell(G, y):
    while True:
        # step 1
        I = sample(range(n), k)
        y_I = matrix(F2, 1, k)      # 1*k
        G_I = matrix(F2, k, k)      # k*k
        for i, col in enumerate(I):
            y_I[:, i] = y[:, col]
            G_I[:, i] = G[:, col]
        if rank(G_I) != k:  # has no inverse
            continue
        invG_I = G_I^-1             # k*k
        G_bar = invG_I * G          # k*k * k*n = k*n
        # step 2
        y_bar = y - y_I * G_bar
        # step 3
        x = F2.list()[1:]  # F_2 / {0} = [1]
        for ai in range(k):    # size-1 subset in I.
            g = matrix(x[0] * G_bar[ai])
            e = y_bar - g
            wt_e = GetRowVectorWeight(e)
            # print wt_e
            if wt_e == t:
                return e

c0 = ciphers[0]
e = lee_brickell(pubkey, c)

然后直接代入（被引入了一些error的）密文c0进这个算法，就能求出来这个error。

接着， $$ c - e = (m \cdot G’ + e) - e = m \cdot G’ = c' $$ 然后乘个逆矩阵就完事了。

所以最后完整的exp：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


# sage 8.9

ciphers = load("cipher.sobj")
pubkey = load("pubkey.sobj")

n = 64
k = 28
t = 6
F2 = GF(2)
def GetRowVectorWeight(n):
    return sum(ZZ(i) for i in n[0])

def lee_brickell(G, y):
    while True:
        # step 1
        I = sample(range(n), k)
        y_I = matrix(F2, 1, k)      # 1*k
        G_I = matrix(F2, k, k)      # k*k
        for i, col in enumerate(I):
            y_I[:, i] = y[:, col]
            G_I[:, i] = G[:, col]
        if rank(G_I) != k:  # has no inverse
            continue
        invG_I = G_I^-1             # k*k
        G_bar = invG_I * G          # k*k * k*n = k*n
        # step 2
        y_bar = y - y_I * G_bar
        # step 3
        x = F2.list()[1:]  # F_2 / {0} = [1]
        for ai in range(k):    # size-1 subset in I.
            g = matrix(x[0] * G_bar[ai])
            e = y_bar - g
            wt_e = GetRowVectorWeight(e)
            # print wt_e
            if wt_e == t:
                return e

s = ""
for c in ciphers:
    e = lee_brickell(pubkey, c)  # c = m * pubkey + e
    corrected = c - e            # m * pubkey = c - e
    m = pubkey.solve_left(corrected)
    for i in m[0]:
        s += str(i)
# print s

print hex(int(s, 2)).strip('0xL').decode('hex')
# flag{c941a3cc-85e3-4401-a0f1-764206e71bf3}

后来意识到用官方给的函数为什么会报错的原因后，改用官方的也写了一下exp，居然只需要15行：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


# sage 8.9
ciphers = load("cipher.sobj")
pubkey = load("pubkey.sobj")

C = codes.LinearCode(pubkey)
from sage.coding.information_set_decoder import LeeBrickellISDAlgorithm
A = LeeBrickellISDAlgorithm(C, (6,6))

s = ""
for cipher in ciphers:
    corrected = A.decode(cipher[0])    # c = m * pubkey + e ==> c' = m * pubkey
    m = pubkey.solve_left(corrected)
    s += ''.join(str(i) for i in m)

print hex(int(s, 2)).strip('0xL').decode('hex')
# flag{c941a3cc-85e3-4401-a0f1-764206e71bf3}

总结一下，感觉自己还是太菜了啊。。

对于这种未知的东西，总有一种畏惧感？？

资料太多了，一时不知道到底怎么看。。现学能力有待提高。

todo: https://crypto.stackexchange.com/questions/15107/mceliece-information-set-decoding-attack-vulnerability/22779#22779

pell

这个proof of work，很眼熟啊，感觉是杭电的师傅出的题。

在"A Friendly Introduction to Number Theory"的第32章有讲过这个pell equation。

意思就是说，如果你找到了这个方程的一个最小（正整数）解，那么你就可以通过一个类似于通项公式的方式递推得到所有的解。

证明的话，嘿嘿嘿，当初我看的时候就没怎么看得懂，似乎是用了一个非常高超的数学证明手法：费马的无穷递降法（Fermat’s method of descent）。。。数论还是很有意思的啊。

但是好在有一个online website能够帮我们解决这种二次的丢番图方程（Diophantine equations）： https://www.alpertron.com.ar/QUAD.HTM （这个网站上面的因数分解功能也很给力，基本280bit以下的都能通过ECM或者Quadratic Sieve在短时间内分解出来）。

这一题中的方程形式是 $$ x^2 - a y^2 = b $$

其中a, b的取值如下：

1
2


a = random.randint(10,50)
b = random.randint(1,2)

一共就只有41*2 == 82种可能，但是由于pell equations是在有些情况下是没有解的（b = 2的时候经常会没解），在某些情况下最小解会挺大的，所以服务器给出某一组a, b的时候是有可能无解的。。。

wiki上就给出了在b = 1的时候，最小解的情况，~~但没有给出递推公式（也可以自己推算一下）~~（经某位师傅提醒，wiki上实际上是有递推公式的。。）。

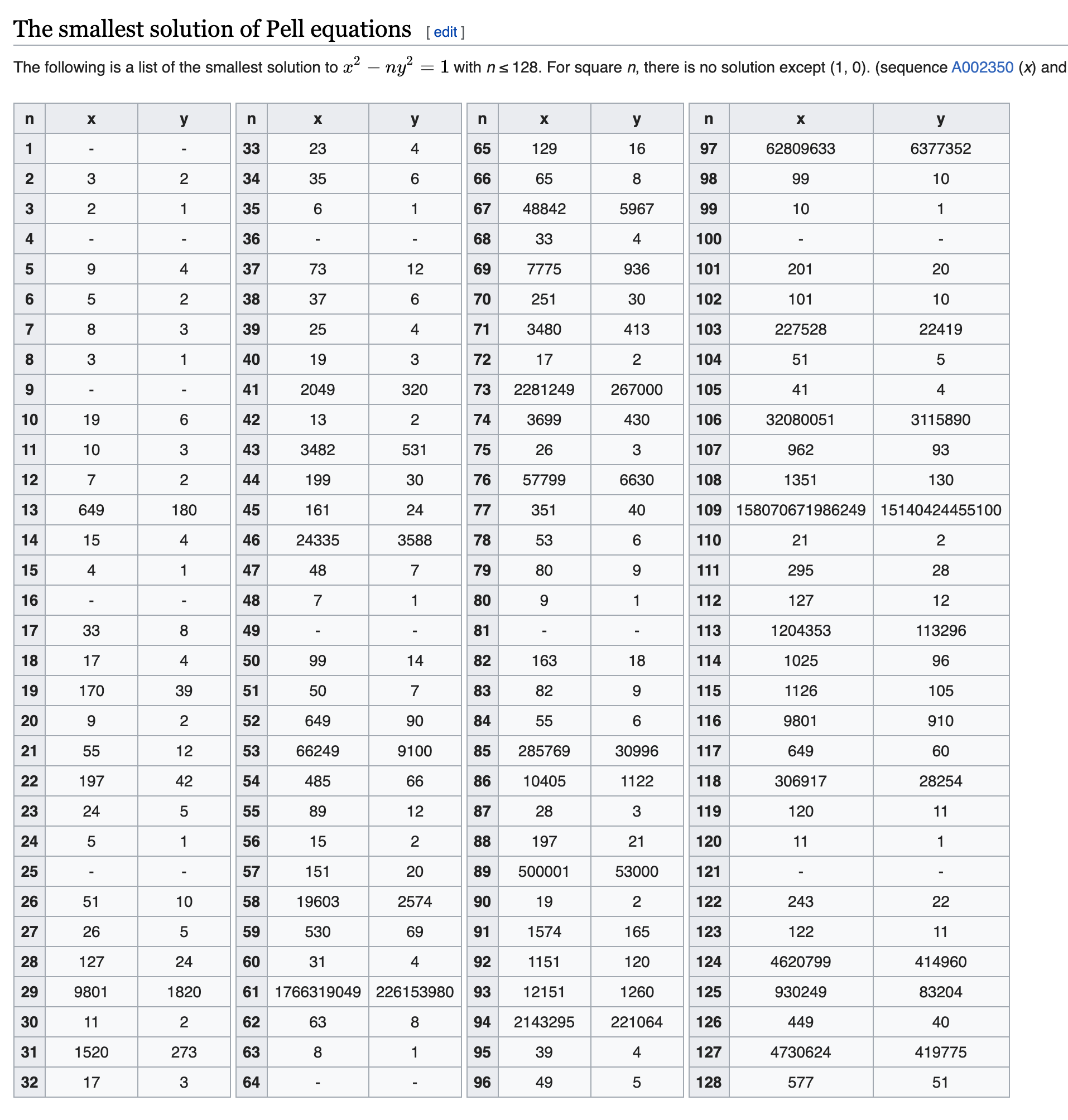
在这个神奇的网站上是有递推公式的，例如a = 24, b = 1的时候，我们可以得到如下结果：

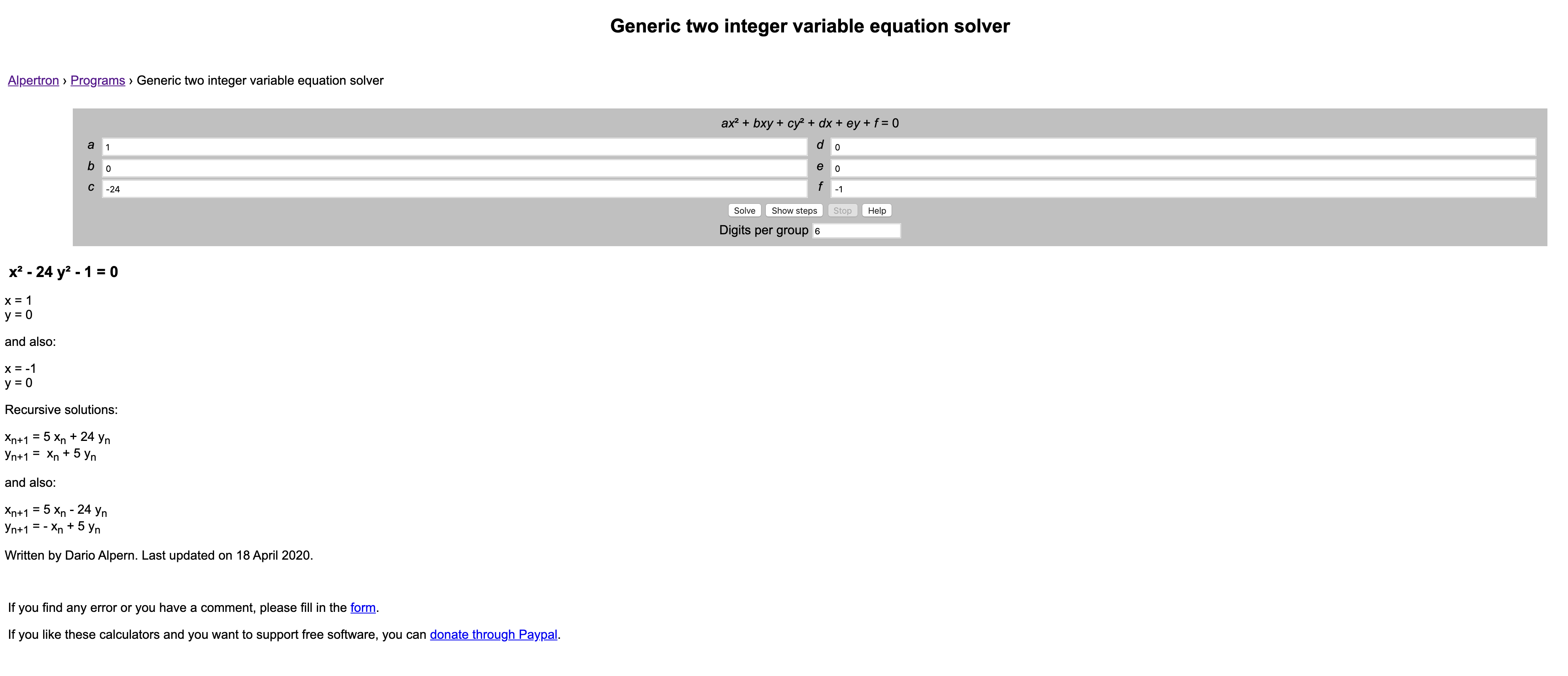
我们可以从x = 1, y = 0这个解（显然这是b==1时都有的一个trivial solution）开始，然后通过 $$ \begin{aligned} x_{n+1} &= 5 ⁢x_n + 24 ⁢y_n \newline y_{n+1} &= x_n + 5 ⁢y_n \end{aligned} $$ 这个递推公式求出后面的所有解。

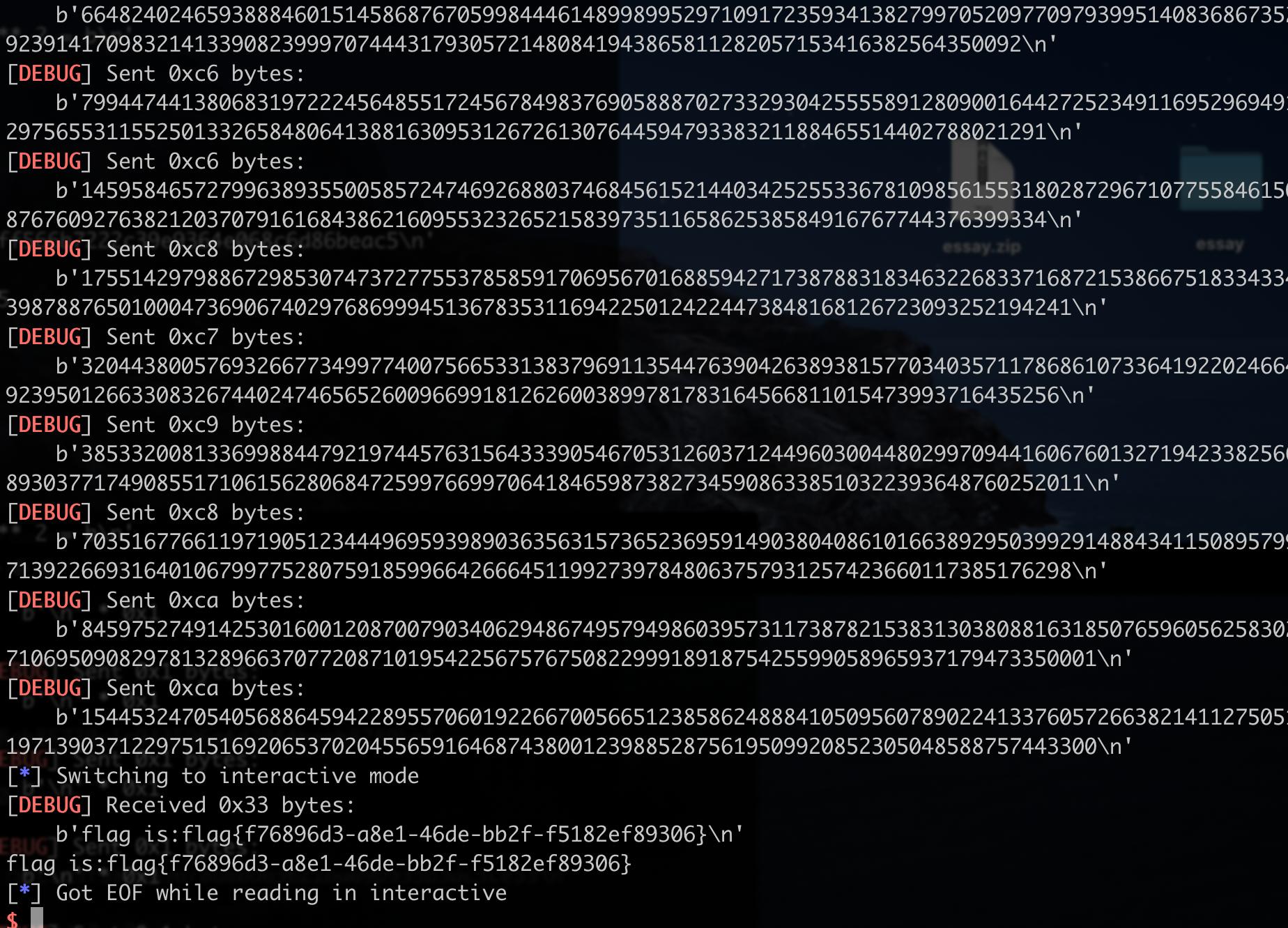
这一题，只需要给服务器发送150个解就可以了。

但由于是需要nc远程交互的，而且我也没怎么找到那个网站的api，所以就先预先算好一些比较小一点的递归公式，然后当服务器给出的参数与本地相符时，就进行交互，否则，断开重连。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81


import re
from hashlib import sha256
from itertools import product
import time
from pwn import *


context.log_level = "debug"
s = string.ascii_letters + string.digits
while True:
    r = remote('39.97.210.182', 61235)

    rec = r.recvline().decode()

    suffix = re.findall(r'\(XXXX\+(.*?)\)', rec)[0]
    digest = re.findall(r'== (.*?)\n', rec)[0]
    print(f"suffix: {suffix} \ndigest: {digest}")

    print('Calculating hash...')
    for i in product(s, repeat=4):
        prefix = ''.join(i)
        guess = prefix + suffix
        if sha256(guess.encode()).hexdigest() == digest:
            print(guess)
            break
    r.sendafter(b'Give me XXXX:', prefix.encode())

    rec = r.recvlines(numlines=2)[1].decode()
    a = int(re.findall(r'a = ([0-9].*?),', rec)[0])
    b = int(re.findall(r'b = ([0-9].*?)', rec)[0])

    print(a, b)
    if a == 35 and b == 1:
        x, y = 1, 0
        for _ in range(150):
            x, y = 6*x + 35*y, x + 6*y
            r.sendline(str(abs(x)).encode())
            time.sleep(0.3)
            r.sendline(str(abs(y)).encode())
            time.sleep(0.3)

    elif a == 30 and b == 1:
        x, y = 1, 0
        for _ in range(150):
            x, y = 11*x + 60*y, 2*x + 11*y
            r.sendline(str(abs(x)).encode())
            time.sleep(0.3)
            r.sendline(str(abs(y)).encode())
            time.sleep(0.3)

    elif a == 24 and b == 1:
        x, y = 1, 0
        for _ in range(150):
            x, y = 5*x + 24*y, 1*x + 5*y
            r.sendline(str(abs(x)).encode())
            time.sleep(0.3)
            r.sendline(str(abs(y)).encode())
            time.sleep(0.3)

    elif a == 20 and b == 1:
        x, y = 1, 0
        for _ in range(150):
            x, y = 9*x + 40*y, 2*x + 9*y
            r.sendline(str(abs(x)).encode())
            time.sleep(0.3)
            r.sendline(str(abs(y)).encode())
            time.sleep(0.3)

    elif a == 15 and b == 1:
        x, y = 1, 0
        for _ in range(150):
            x, y = 4*x + 15*y, 1*x + 4*y
            r.sendline(str(abs(x)).encode())
            time.sleep(0.3)
            r.sendline(str(abs(y)).encode())
            time.sleep(0.3)

    else:
        r.close()
        continue
    r.interactive()

sleep(0.3)的原因是，我先在本地测试的时候，发现如果不sleep的话，可能会有客户端发送过快，导致多条内容到了服务端后会变成一条，然后int解析不了。。

invalid literal for int() with base 10: '47525\n9701\n'

最后开了n个终端在跑，跑出来如下：