所有附件: https://mega.nz/file/ObxVnK4S#9p9L9bohqgkyupBtM2a0geVvDFBAcDEC7KyC4U9OD4g
==Difficulty: intuitive==
The plaintext is a string of meaningful lowercase letters, without whitespace.
Please submit the result with "NCTF{}" wrapped.
==Author: Soreat_u==
毕竟校赛,总得出一道送分题。
ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee
不难发现这些字母都是键盘上英文字母第一排的。

不难想到,这些字母就对应着数字1, 2, 3, ..., 9。
q -> 1
w -> 2
e -> 3
r -> 4
t -> 5
y -> 6
u -> 7
i -> 8
o -> 9
每个字母出现的次数都在1-4这个范围内,再根据题名Keyboard,不难再联想到九宫格键盘。

那么答案就很明显了。
贴脚本:
1
2
3
4
5
6
7
8
9
|
cipher = 'ooo yyy ii w uuu ee uuuu yyy uuuu y w uuu i i rr w i i rr rrr uuuu rrr uuuu t ii uuuu i w u rrr ee www ee yyy eee www w tt ee'
s = ' qwertyuiop'
d = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz']
for part in cipher.split(' '):
# print(part)
count = len(part)
num = s.index(part[0])
print(d[num][count - 1], end='')
|
得到youaresosmartthatthisisjustapieceofcake
加上NCTF{}即为flag:NCTF{youaresosmartthatthisisjustapieceofcake}
是不是有点太脑洞了?但是题名的提示已经很明显了,这点脑洞总应该有的吧?
==Difficulty: easy==
Can you break the “unbreakable” cipher?
==Author: Soreat_u==
灵感来源于西湖论剑线下赛的一道密码题VVVV。
本题是一个扩展版(字母表从26个小写字母扩展到52个大小写字母)的Vigenere Cipher,挺简单的啊。
具体分析见我写的Cryptanalysis of Vigenere Cipher: http://www.soreatu.com/essay/Cryptanalysis
of Vigenere Cipher.html
可以参考上面我写的Cryptanalysis of Vigenere Cipher。
不过,Google随便搜一个Vigenere Cipher decoder: https://www.guballa.de/vigenere-solver
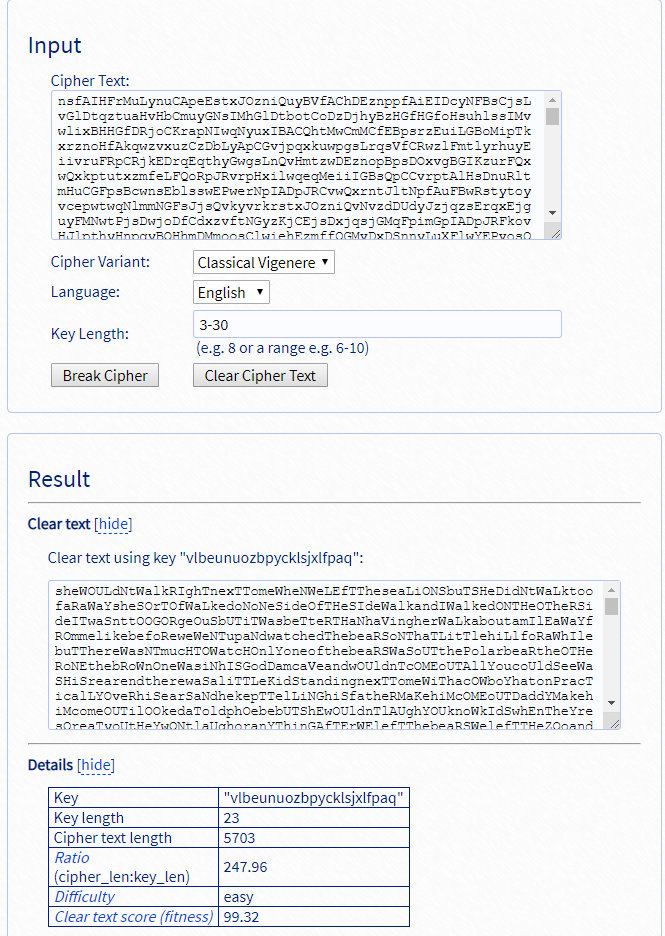
都能秒解。
区分一下大小写就能出flag了。
NCTF{vlbeunuozbpycklsjXlfpaq}
==Difficulty: baby==
I forget the modulus. Can you help me recover it?
==Author: Soreat_u==
主要考察对RSA几个参数之间关系的理解。
本题考点在于,如何从加密指数e和解密指数d中算出p, q ,进而恢复出模数n。
如果已知e, d, n,是可以很轻松地按照下面这个算法算出两个大质数p, q的:

然而本题没有给出n,而且要求的就是n,所以这个算法不可行。
本题需要从RSA的这几个参数之间的关系出发去思考。
只要算出$n$即可解密。
首先有,
$$
e\cdot d \equiv 1 \quad (\text{mod}\ \phi(n))
$$
将同余式改写成等式,
$$
e\cdot d = k\cdot \phi(n) + 1
$$
其中$k$为整数,我们先来估算一下$k$的大致范围。
也就是,
$$
e\cdot d - 1 = k\cdot \phi(n)
$$
等式左边均已知,等式右边是$\phi(n)$的倍数。
实际上,
$$
\phi(n) \approx n, e = 65537, d < n
$$
所以
$$
k < e = 65537
$$
只需穷举小于65537且能整除$ed - 1$的所有$k$,即可得到所有可能的$\phi(n)$
而本题使用的$p, q$十分接近(相差几百左右)。
在算出可能的$\phi(n)$后,可以尝试求p, q:
$$
(p-1)^2 < \phi(n) = (p - 1)(q - 1) < (q - 1)^2
$$
如果尝试对$\phi(n)$开根取整,再在这个根的附近($\pm2000$)去寻找能够整除$\phi(n)$的数,如果找到了,那么基本上就是$p-1$或者$q-1$。
有了$p-1$,就能算出$p$和$q$,相乘即可得到$n$。有了$c, d, n$,直接解密即可得到flag。
需要gmpy2库,安装可参考pcat - gmpy2安装使用方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#!/usr/bin/python2
from Crypto.Util.number import *
import gmpy2
e = 65537
d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
kphi = e*d - 1
for k in range(1, e):
if kphi % k == 0:
phi = kphi // k
root = gmpy2.iroot(phi, 2)[0]
for p in range(root - 2000, root + 2000):
if phi % (p-1) == 0: break
else: continue
break
q = phi//(p-1) + 1
m = pow(c, d, p*q)
print(long_to_bytes(m))
# 'NCTF{70u2_nn47h_14_v3ry_gOO0000000d}'
|
大概3s内就能得出flag。
这一题,还是希望大家能够对RSA的几个参数之间的关系有一个深入的了解。
==Difficulty: baby==
3072-bit RSA moduli are sufficiently sucure in several years. How about this 10240-bit one?
==Author: Soreat_u==
最近在看一些整数分解的算法,其中有一个就是Pollard's p-1 method。
前几天又正好在先知社区上看到了一篇Pollard's rho algorithm的文章: https://xz.aliyun.com/t/6703
,联想到一个Pollard's p-1 method。
An Introduction to Mathematical Cryptography书中说到:

有的时候(极少情况),RSA模数的位数越高并不意味着安全性越高。
存在一些比较特殊的模数,很容易被分解。
这个分解算法就叫做Pollard's p-1 method。
于是,就根据这个算法出了这一道题。
这一题的关键是如何将分解n成两个5120位的大质数p, q。
首先,p,q由getPrime函数生成:
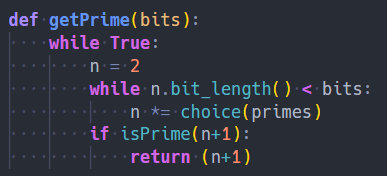
其中,primes是Crypto.Util.number模块中定义的前10000个质数。在VScode中按F12即可跳转到定义处。
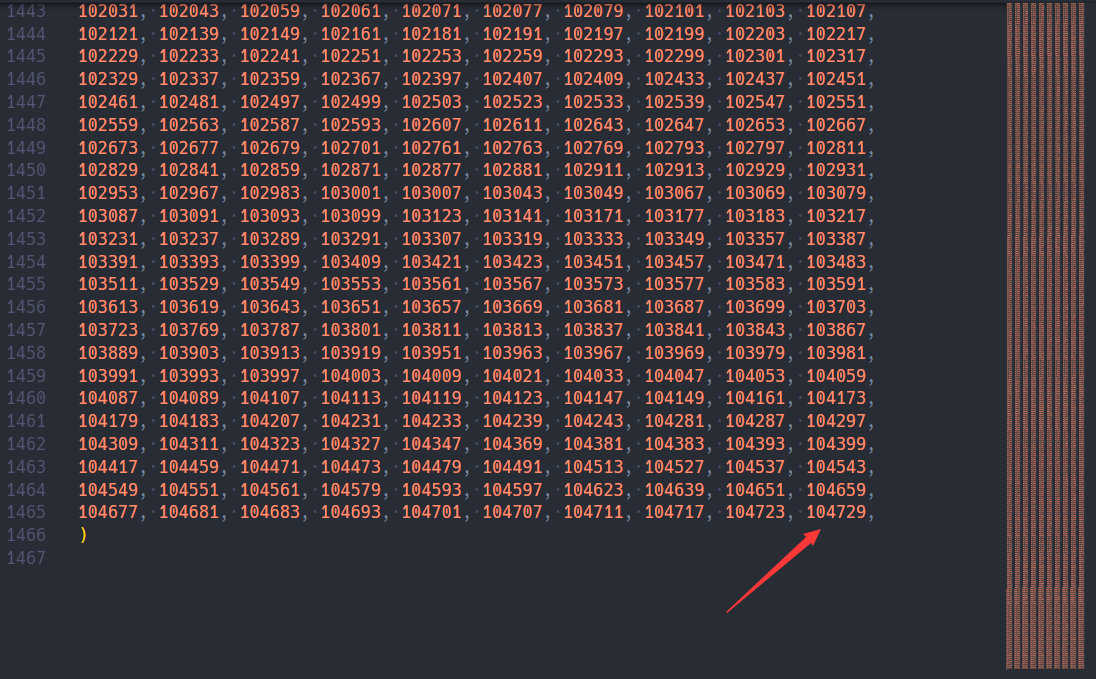
可以看到,最大的质数是104729。
一般来说,我们寻找大质数都是随机生成一个大数,然后将其经过素性测试,能够通过的就返回。
但是这一题里面,并不是这样生成的。
我们可以看到,getPrime生成的质数,都是由前10000个质数累乘起来然后再加1生成的。
这就使得生成的质数p,将其减一后,其结果(也就是这个质数的欧拉函数p-1)能够被分解为许多个相对来说很小的质数。这在数学上有一个专门的术语,叫做B-smooth。很显然,p是104729-smooth的。
关于smooth number的定义,请参考wiki: https://en.wikipedia.org/wiki/Smooth_number
smooth有什么坏处呢?
我们先来看一个叫做费马小定理的东西:
$$
a^{p-1} \equiv 1 \quad (\text{mod}\ p)
$$
也就是说,指数那边每增加 $p-1$,其结果仍然不变。指数以 $p-1$ 为一个循环。
我们将其变形一下,
$$
a^{p-1} - 1 \equiv 0 \quad (\text{mod}\ p)
$$
模p同余0,也就是说 $a^{p-1} - 1$ 是 $p$ 的倍数。
将同余式改写为等式,
$$
a^{t \times (p-1)} - 1 = k\times p
$$
其中 $t, k$ 是两个整数。
如果指数$exp$是 $p-1$ 的倍数,那么$a^{exp} - 1 $就会是 $p$ 的倍数。
上面的$p$均指某一个质数,而非N = pq中的p
这里很关键。
如果我们能够找到一个指数$L$,使得对于某一个底数$a$,$a^{L} - 1$ 是p的倍数,但不是q的倍数。
这时,我们只要去计算
$$
gcd(a^{L}-1, N)
$$
得到的结果,必定是p。也就是说,我们成功地分解了N。
那么,怎么去找到这个$L$呢?
Pollard的厉害之处就在于此,他发现,如果p-1正好是一些很小的质数的乘积,那么p-1就能整除$n!$,其中$n$是一个不太大的数。
为什么呢?说下我自己的理解。
假设p-1是p1, p2, ..., pk这些质数的乘积,其中最大的质数是pk。那么,很显然pk!=1·2·...·pk肯定包括了p1, p2, ..., pk这些质数的乘积,pk!肯定是p-1的倍数。
也就是说,$n > pk$ 的时候,$n!$很大概率上就能被p-1整除。(考虑到p1, p2, ..., pk中可能有重复的情况)
这导致了Pollard' p-1 method:
对于每一个$n = 2, 3, 4, …$,我们任意选择一个底数$a$(事实上,我们可以简单地选择为2),并计算
$$
gcd(a^{n!-1}, N)
$$
如果结果落在1和$N$中间,那么我们就成功了。

实际操作中,这个算法有很多可以优化的地方。
例如,我们并不需要算出$a^{n!-1}$的确切值,当$n>100$时,$n!$本身就已经很大了,整体结果肯定巨大无比。我们每一次只需要算出$a^{n!-1}\ \text{mod}\ N$的值即可,可以将运算结果限制在模$N$的范围内。
这一题,实际上我们已经知道了最大的质数为104729,我们大概只需要算到$n = 104729$就可以了(不考虑p-1的构成中有几个重复的比较大的质数)。
并不需要每一个$n$都去算一遍$gcd(a^{n!-1}, N)$,每隔一个恰当的间隔去算就可以了。
先自己照着算法流程实现一下Pollard's p-1 method:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
from Crypto.Util.number import *
def Pollard_p_1(N):
a = 2
while True:
f = a
# precompute
for n in range(1, 80000):
f = pow(f, n, N)
for n in range(80000, 104729+1):
f = pow(f, n, N)
if n % 15 == 0:
d = GCD(f-1, N)
if 1 < d < N:
return d
print(a)
a += 1
|
然后就直接去分解这个10000+位的N。
1
2
|
n = 1592519204764870135...
print( Pollard_p_1(n) )
|
大概跑个十几分钟(由于这个N太大了,十万次左右的快速幂还是需要点时间的),能分解出来:

后面就是正常的RSA解密了。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
from Crypto.Util.number import *
n = 1592519204764870135...
c = 5744608257563538066...
p = 5075332621067110585...
q = n // p
assert(p*q == n)
d = inverse(0x10001, (p-1)*(q-1))
m = pow(c, d, n)
print(long_to_bytes(m))
# b'NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}'
|
出这一道题的目的,还是希望能让大家去深入了解某些算法背后的原理。
不过看大家好像都是用yafu直接分解的。。。。而且还挺快的。
后面应该会写一篇总结各种因数分解算法的文章的。
==Difficulty: easy==
DES has a very bad key schedule.
==Author: Soreat_u==
当初在学DES
的时候,就意识到DES的Key schedule是可以直接逆回去的。
具体的DES算法: https://csrc.nist.gov/csrc/media/publications/fips/46/3/archive/1999-10-25/documents/fips46-3.pdf
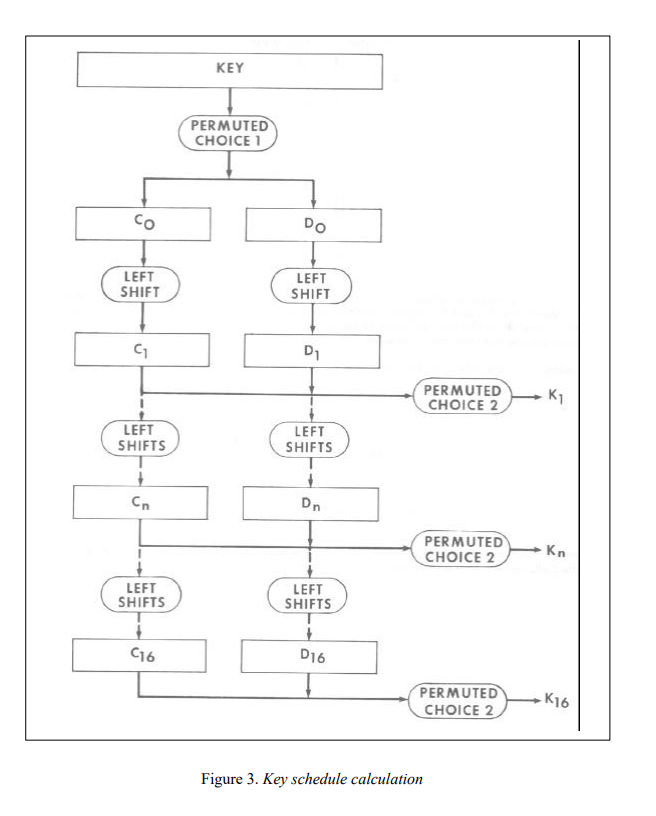
leak出的Kn[10]应该是第11组子密钥$K_{11}$。
PERMUTED CHOICE 2是一个56 bits -> 48 bits的置换。可以穷举被truncated的8bits,逆一下对$K_{11}$的PERMUTED CHOICE 2即可返回到C11 D11。
再沿着那个长流程顺下去(Ci, Di经过16次LEFT SHIFTS后会复原),就可以恢复出所有子密钥。
贴上半年前写的exp.py:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
from base64 import b64decode
from itertools import product
from DES import * # https://github.com/soreatu/Cryptography/blob/master/DES.py
guess_8bit = list(product(range(2), repeat=8))
not_in_PC2 = [9,18,22,25,35,38,43,54]
def re_PC2(sbkey):
# 48-bit -> 56-bit
res = [0]*56
for i in range(len(sbkey)):
res[PC_2_table[i]-1] = sbkey[i]
return res # ok
def guess_CiDi10(sbkey, t):
res = re_PC2(sbkey)
for i in range(8):
res[not_in_PC2[i]-1] = guess_8bit[t][i]
return res # ok
def guess_allsbkey(roundkey, r, t):
sbkey = [[]]*16
sbkey[r] = roundkey
CiDi = guess_CiDi10(roundkey, t)
Ci, Di = CiDi[:28], CiDi[28:]
for i in range(r+1,r+16):
Ci, Di = LR(Ci, Di, i%16)
sbkey[i%16] = PC_2(Ci+Di)
return sbkey # ok
def long_des_enc(c, k):
assert len(c) % 8 == 0
res = b''
for i in range(0,len(c),8):
res += DES_enc(c[i:i+8], k)
return res
def try_des(cipher, roundkey):
for t in range(256):
allkey = guess_allsbkey(roundkey, 10, t)
plain = long_des_enc(cipher, allkey[::-1])
if plain.startswith(b'NCTF'):
print(plain)
if __name__ == "__main__":
cipher = b64decode(b'm0pT2YYUIaL0pjdaX2wsxwedViYAaBkZA0Rh3bUmNYVclBlvWoB8VYC6oSUjfbDN')
sbkey10 = [0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1]
try_des(cipher, sbkey10)
# b'NCTF{1t_7urn3d_0u7_7h47_u_2_g00d_@_r3v3rs3_1snt}'
|
==Difficulty: simple==
We can do RSA decryption even if e and phi(n) are not coprime.
Hint: m has exactly 24196561 solutions :)
Hint2: https://stackoverflow.com/questions/6752374/cube-root-modulo-p-how-do-i-do-this
Hint3: https://arxiv.org/pdf/1111.4877.pdf
==Author: Soreat_u==
此题灵感来自于hackergame 2019的一道十次方根题。那一题当时从下午2、3点一直做到了晚上12点,终于在将近10个小时的搜寻、推算之后,解了出来,印象十分深刻,也学到很多很多东西。
那道题主要要解决的一个问题就是,如何在有限域内开10次方根。
当时几乎翻了上十篇paper,才在https://arxiv.org/pdf/1111.4877.pdf这篇paper里找到了一个比较容易实现的算法。
做完后,思考了下,发现能够扩展到RSA上面。
我们知道,RSA对参数的一个要求就是,e和phi(n)一定要互素。这是为了要让e在模phi(n)下存在逆元d,进而可以直接pow(c, d, n)来解密。
那如果e和phi(n)不互质就会无解么?不,事实上,有解而且不止有一解。
这一题就是基于这个观察而出的。
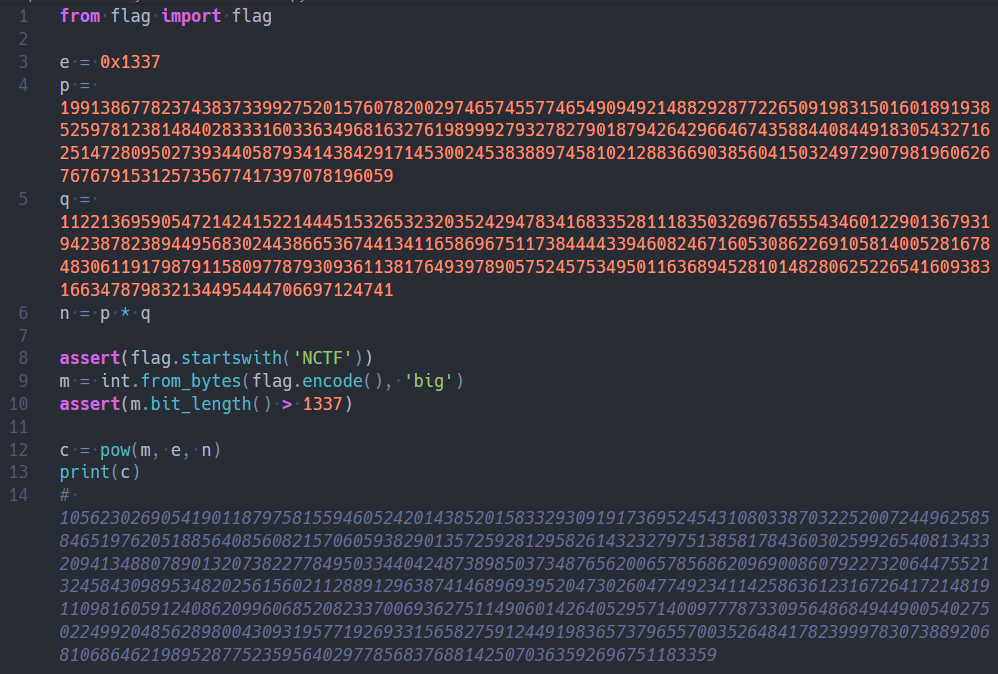
题面十分简洁,甚至都给出了p, q。乍一看,肯定觉得这是一道送分题,然而事实远非如此。
正常情况下的RSA都要求e和phi(n)要互素,不过也有一些e和phi(n)有很小的公约数的题目,这些题目基本都能通过计算e对phi(n)的逆元d来求解。
然而本题则为e和p-1(或q-1)的最大公约数就是e本身,也就是说e | p-1,只有对c开e次方根才行。
可以将同余方程
$$
m^e \equiv c \quad (\text{mod}\ n)
$$
化成
$$
\begin{aligned}
m^e &\equiv c \quad (\text{mod}\ p)\newline
m^e &\equiv c \quad (\text{mod}\ q)
\end{aligned}
$$
然后分别在GF(p)和GF(q)上对c开e=0x1337次方根,再用CRT组合一下即可得到在mod n下的解。
问题是,如何在有限域内开根?
这里e与p-1和q-1都不互素,不能简单地求个逆元就完事。
这种情况下,开平方根可以用Tonelli–Shanks algorithm,wiki
说这个算法可以扩展到开n次方根。
在这篇paper
里给出了具体的算法:Adleman-Manders-Miller rth Root Extraction Method
应该还有其他的算法。。不过这一个对我来说比较容易去implement。

这个算法只能开出一个根,实际上开0x1337次方,最多会有0x1337个根(这题的情况下有0x1337个根)。
如何找到其他根?
StackOverflow - Cube root modulo P
给出了方法:

如何找到所有的primitve 0x1337th root of 1?
StackExchange - Finding the n-th root of unity in a finite field
给出了方法:

- 先用
Adleman-Manders-Miller rth Root Extraction Method在GF(p)和GF(q)上对c开e次根,分别得到一个解。大概不到10秒。
- 然后去找到所有的
0x1336个primitive nth root of 1,乘以上面那个解,得到所有的0x1337个解。大概1分钟。
- 再用
CRT对GF(p)和GF(q)上的两组0x1337个解组合成mod n下的解,可以得到0x1337**2==24196561个mod n的解。最后能通过check的即为flag。大概十几分钟。
exp.sage如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
|
import random
import time
# About 3 seconds to run
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def findAllPRoot(p, e):
print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p))
start = time.time()
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
end = time.time()
print("Finished in {} seconds.".format(end - start))
return proot
def findAllSolutions(mp, proot, cp, p):
print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p))
start = time.time()
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
end = time.time()
print("Finished in {} seconds.".format(end - start))
return all_mp
c = 10562302690541901187975815594605242014385201583329309191736952454310803387032252007244962585846519762051885640856082157060593829013572592812958261432327975138581784360302599265408134332094134880789013207382277849503344042487389850373487656200657856862096900860792273206447552132458430989534820256156021128891296387414689693952047302604774923411425863612316726417214819110981605912408620996068520823370069362751149060142640529571400977787330956486849449005402750224992048562898004309319577192693315658275912449198365737965570035264841782399978307388920681068646219895287752359564029778568376881425070363592696751183359
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
e = 0x1337
cp = c % p
cq = c % q
mp = AMM(cp, e, p)
mq = AMM(cq, e, q)
p_proot = findAllPRoot(p, e)
q_proot = findAllPRoot(q, e)
mps = findAllSolutions(mp, p_proot, cp, p)
mqs = findAllSolutions(mq, q_proot, cq, q)
print mps, mqs
def check(m):
h = m.hex()
if len(h) & 1:
return False
if h.decode('hex').startswith('NCTF'):
print(h.decode('hex'))
return True
else:
return False
# About 16 mins to run 0x1337^2 == 24196561 times CRT
start = time.time()
print('Start CRT...')
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if check(solution):
print(solution)
print(time.time() - start)
end = time.time()
print("Finished in {} seconds.".format(end - start))
|
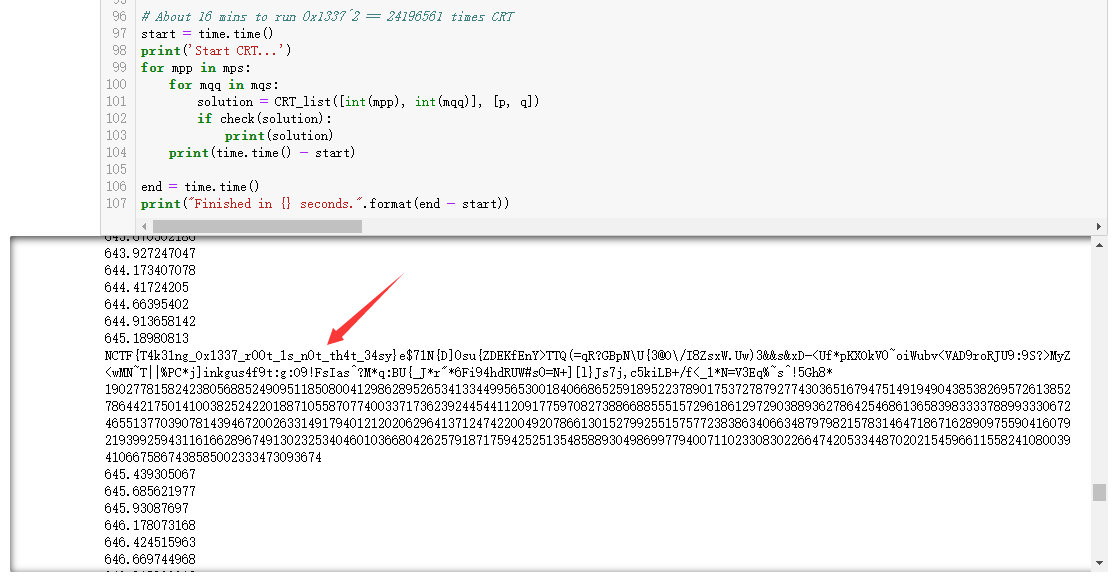
2019.12.04更新:
直接用sagemath求0x1337次方根,大概1h也能跑出来:

2020.08.11更新:
AMM算法中计算离散对数部分有些问题,已修改,但还未测试。
p, q都是预先用下面这个函数生成的,保证了e | p-1, e | q-1。
1
2
3
4
5
6
7
8
|
import random
from Crypto.Util.number import *
def gen():
p = e * random.getrandbits(1012) + 1
while not isPrime(p):
p = e * random.getrandbits(1012) + 1
return p
|
而且p-1, q-1的ord(e) = 1,使得Adleman-Manders-Miller rth Root Extraction Method中无需计算DLP。降低了题目难度。
flag后面填充了一段杂乱的字符串,是为了增加flag转成整数后的位数。不然位数太低,算出GF(p)和GF(q)里2组0x1337个解,取交集就可以得到flag了。位数增加后,就必须要算24196561次CRT才能得到flag,可能需要个十几分钟来跑。
==Difficulty: interesting==
不知道大家信安数基学的怎么样
nc 139.129.76.65 60001
The script to pass proof of work is provided in the link.
Have fun :>
==Author: Soreat_u==
最近在看随机数,里面有一个方法就是LCG(线性同余生成器)。
$$
N_{i+1} \equiv a\cdot N_{i} + b \quad \text{mod}\ \ m
$$
在 https://zeroyu.xyz/2018/11/02/Cracking-LCG/
里,作者详细地描述了4种针对各种参数已知情况的攻击。本题就是基于这篇文章而出的。
具体分析可以参考: https://zeroyu.xyz/2018/11/02/Cracking-LCG/
。
直接贴exp.py:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
|
# python2
import hashlib
import primefac
from pwn import *
from Crypto.Util.number import *
host, port = '', 10000
r = remote(host, port)
# context.log_level = 'debug'
def proof_of_work():
print '[+] Proof of work...'
r.recvuntil('hexdigest() = ')
digest = r.recvline().strip()
r.recvuntil("s[:7].encode('hex') =")
prefix = r.recvline().strip().decode('hex')
# s = r.recvline().strip()
for suffix in range(256**3):
guess = prefix + long_to_bytes(suffix, 3)
if hashlib.sha256(guess).hexdigest() == digest:
print '[+] find: ' + guess.encode('hex')
break
r.recvuntil("s.encode('hex') = ")
# r.sendline(s)
r.sendline(guess.encode('hex'))
def solve1(N, a, b, n1):
return (n1 - b) * inverse(a, N) % N
def solve2(N, a, n1, n2):
b = (n2 - n1 * a) % N
return solve1(N, a, b, n1)
def solve3(N, n1, n2, n3):
a = (n3 - n2) * inverse(n2 - n1, N) % N
return solve2(N, a, n1, n2)
def solve4(n1, n2, n3, n4, n5, n6):
t1 = n2 - n1
t2 = n3 - n2
t3 = n4 - n3
t4 = n5 - n4
t5 = n6 - n5
N = GCD(t3*t1 - t2**2, t5*t2 - t4*t3)
factors = primefac.factorint(N)
while not isPrime(N):
for prime, order in factors.items():
if prime.bit_length() > 128:
continue
N = N / prime**order
return solve3(N, n1, n2, n3)
def challenge1():
print '[+] Solving challenge1...'
r.recvuntil('lcg.N = ')
N = int(r.recvline().strip())
r.recvuntil('lcg.a = ')
a = int(r.recvline().strip())
r.recvuntil('lcg.b = ')
b = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next1 = int(r.recvline().strip())
init_seed = solve1(N, a, b, next1)
r.recvuntil('lcg.seed = ')
r.sendline(str(init_seed))
def challenge2():
print '[+] Solving challenge2...'
r.recvuntil('lcg.N = ')
N = int(r.recvline().strip())
r.recvuntil('lcg.a = ')
a = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next1 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next2 = int(r.recvline().strip())
init_seed = solve2(N, a, next1, next2)
r.recvuntil('lcg.seed = ')
r.sendline(str(init_seed))
def challenge3():
print '[+] Solving challenge3...'
r.recvuntil('lcg.N = ')
N = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next1 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next2 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next3 = int(r.recvline().strip())
init_seed = solve3(N, next1, next2, next3)
r.recvuntil('lcg.seed = ')
r.sendline(str(init_seed))
def challenge4():
print '[+] Solving challenge4...'
r.recvuntil('lcg.next() = ')
next1 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next2 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next3 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next4 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next5 = int(r.recvline().strip())
r.recvuntil('lcg.next() = ')
next6 = int(r.recvline().strip())
init_seed = solve4(next1, next2, next3, next4, next5, next6)
r.recvuntil('lcg.seed = ')
r.sendline(str(init_seed))
proof_of_work()
challenge1()
challenge2()
challenge3()
challenge4()
r.interactive()
|
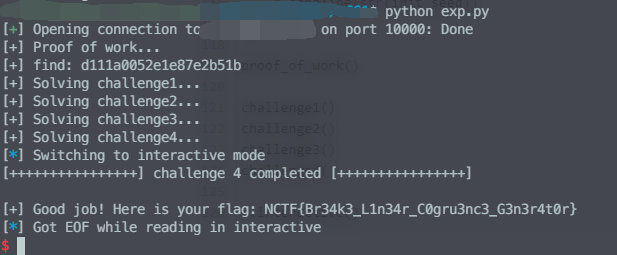
这些东西,信安数基书上都写得明明白白的,可不要白学了。
















