Random number generators are a key part of web security. They are used all over the place, from session tokens to tokens to sent to an email address to verify its owner made a particular request, to CAPTCHA tokens and so on. In all these applications, if the token can be predicted, then the security mechanism can be broken, and a malicious user will be able to identify themselves as someone who they are not.
What I won’t talk about in this series is anything about the maths of random number generators, beyond explaining how the algorithms are implmented. Why a particular algorithm makes a good PRNG is beyond the scope of this series.
In practice: Java’s default random number generator, java.util.Random.
Internel state(seed): one single number.
Precision: 48 bits (in Java’s case).
递推公式:
$$
\text{seed} = (\text{seed} \times \text{multiplier} + \text{addend}) \quad \text{mod} \ 2^\text{precision}
$$
or
$$
N_{i+1} = a \cdot N_{i} + b \quad \text{mod}\ n
$$
multiplier = 25214903917, addend = 11 in Java’s case.
The mod operation is implemented using a bitmask, (1<<48) - 1
random.nextInt()只取48-bit输出的前36bits。
Java中由于multiplier, addend均已知,只需知道连续两次的输出,即可推出seed。
1
2
3
4
5
6
7
8
9
10
|
Random random = new Random();
long v1 = random.nextInt();
long v2 = random.nextInt();
for (int i = 0; i < 65537; i++) {
long seed = v1 << 16 + i;
if (((seed * multiplier + addend) & mask) >>> 16) == v2) {
System.out.println("Seed found: " + seed);
break;
}
}
|
$$
multiplier \times x + addend \equiv res \quad \text{mod} \ m
$$
已知除了 $x$ 外的所有参数,求 $x$ 。
For more details, please refer to Cracking Random Number Generators - Part 2
.
从低位到高位,按位推算。
以Java为例,
1
2
3
4
5
6
7
8
9
|
res -= addend
ans = 0
for i in range(48):
m = 1 << i
b = res & m
ans |= b
if b == m:
s -= multiplier << i
print(ans)
|
一个涵盖了对LCG的常见攻击的文章:
https://tailcall.net/blog/cracking-randomness-lcgs/
The Mersenne Twister was invented in 1997. The most common implementation of it uses an internal state of 624 32-bit words (integers). These integers are handed out sequentially, applying a transform algorithm to each one before handing them out. Once all 624 integers have been handed out, an algorithm is applied to the state, to get the next 624 integers.
This is used by Ruby’s rand() function, Pythons random module, and PHP’s mt_rand() function.
Internel state: 624 32-bit words
Precision: 32 bits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// java
int[] state;
// Iterate through the state
for (i = 0; i < 624; i++) {
// y is the first bit of the current number,
// and the last 31 bits of the next number
int y = (state[i] & 0x80000000) + (state[(i + 1) % 624] & 0x7fffffff);
// first bitshift y by 1 to the right
int next = y >>> 1;
// xor it with the 397th next number
next ^= state[(i + 397) % 624];
// if y is odd, xor with magic number
if ((y & 1L) == 1L) {
next ^= 0x9908b0df;
}
// now we have the result
state[i] = next;
}
|
1
2
3
4
5
6
7
8
|
// Java
currentIndex++;
int tmp = state[currentIndex];
tmp ^= (tmp >>> 11);
tmp ^= (tmp << 7) & 0x9d2c5680;
tmp ^= (tmp << 15) & 0xefc60000;
tmp ^= (tmp >>> 18);
return tmp;
|
逆出所有624个states: 至少需要获取624个连续的输出。
逆每一步小运算:
For more details, please refer to Cracking Random Number Generators - Part 3
.
tmp ^= (tmp >> 18)
10110111010111100111111001110010
00000000000000000010110111010111100111111001110010
10110111010111100101001110100101
reverse: tmp ^= (tmp >> 18)
10110111010111100101001110100101
00000000000000000010110111010111
0110111010111100111111001110010
移位异或运算仍会保留输入值的部分,可以对这些部分移位异或逆回去。
1
2
3
4
5
6
7
8
|
def unBitShiftRightXor(value, shift):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff << (32 - shift)) & 0xffffffff) >> (i * shift)
part = value & part_mask
value ^= part >> shift
i += 1
return value
|
1
2
3
4
5
6
7
8
|
def unBitShiftLeftXor(value, shift, mask):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff >> (32 - shift)) & 0xffffffff) << (i * shift)
part = value & part_mask
value ^= (part << shift) & mask
i += 1
return value
|
从输出可以逆出对应的state:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
def getState(number):
number = unBitShiftRightXor(number, 18) # reverse: tmp ^= (tmp >> 18)
number = unBitShiftLeftXor(number, 15, 0xefc60000) # reverse: tmp ^= (tmp << 15) & 0xefc60000
number = unBitShiftLeftXor(number, 7, 0x9d2c5680) # reverse: tmp ^= (tmp << 7) & 0x9d2c5680
number = unBitShiftRightXor(number, 11) # reverse: tmp ^= (tmp >> 11)
return number
def backtrace(numbers):
"""
Returns the initial state of the MT PRNG based on list of 624 output numbers
"""
assert(len(numbers) == 624)
state = []
for number in numbers:
state.append(getState(number))
return state
|
new state[i]的生成运算:
1
2
3
4
5
6
|
int y = (state[i] & 0x80000000) + (state[(i + 1) % 624] & 0x7fffffff);
int next = y >>> 1;
if ((y & 1L) == 1L) {
next ^= 0x9908b0df;
}
next ^= state[(i + 397) % 624];
|
需要用到old_state[i], old_state[(i + 1) % 624], old_state[(i + 397) % 624]。
实际上这个算法可逆。如果我们知道了new_state[i], old_state[i + 397]那么我们就可以推出old_state[i], old_state[i + 1]的部分内容。
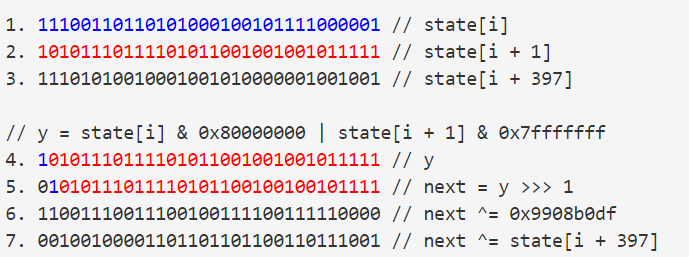
patterns:
i. 第5步的最高位必定为0。
ii. 如果y的最低位为1(奇数),那么会经历第6步,xor with 0x9908b0df,使得第6步结果最高位从0变成1。因此,可以从第6步的结果的最高位是否为1来判断是否xor,也可以判断y的最低位是否为1,也就是old_state[i+1]的最低位是否为1。
从i = 623开始逆推。
7 –> 6:
xor with state[i + 397].
6 –> 5:
取决于结果的最高位是否为1,如果为1,xor with 0x9908b0df。现在已经得到了old_state[i]的最高位和old_state[i+1]的中间30位(除去最高位和最低位)。
5 –> 4: 如果经历了第6步的xor,那么old_state[i + 1]的最低位必定是1,否则就是0。
这样,我们就可以从new_state[i], old_state[i + 397]推出old_state[i]的最高位和old_state[i+1]的低31位。
因此,若要得到old_state[i],先从new_state[i], old_state[i + 397]推出old_state[i]的最高位,再从new_state[i - 1], old_state[i + 396]推出old_state[i]的低31位。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
def getOldStates(new_states):
"""
Returns the old 624 states based on the new 624 states.
"""
states = new_states.copy()
for i in range(623, -1, -1):
tmp = states[i] ^ states[(i + 397) % 624]
if tmp & 0x80000000 == 0x80000000:
tmp ^= 0x9908b0df
res = (tmp & 0x40000000) << 1
tmp = states[(i - 1) % 624] ^ states[(i + 396) % 624]
if tmp & 0x80000000 == 0x80000000:
tmp ^= 0x9908b0df
res |= 1
res |= (tmp & 0x3fffffff) << 1
states[i] = res
return states
|
mt.py文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
from Crypto.Random import random
from Crypto.Util import number
from flag import flag
def convert(m):
m = m ^ m >> 13
m = m ^ m << 9 & 2029229568
m = m ^ m << 17 & 2245263360
m = m ^ m >> 19
return m
def transform(message):
assert len(message) % 4 == 0
new_message = ''
for i in range(len(message) / 4):
block = message[i * 4 : i * 4 +4]
block = number.bytes_to_long(block)
block = convert(block)
block = number.long_to_bytes(block, 4)
new_message += block
return new_message
transformed_flag = transform(flag[5:-1].decode('hex')).encode('hex')
print 'transformed_flag:', transformed_flag
# transformed_flag: 641460a9e3953b1aaa21f3a2
|
一个改过的BitShiftXor运算,需要我们从输出反推输入,直接用前面的unBitShiftRightXor, unBitShiftLeftXor函数即可。
exp.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
from Crypto.Util.number import *
def unBitShiftRightXor(value, shift):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff << (32 - shift)) & 0xffffffff) >> (i * shift)
part = value & part_mask
value ^= part >> shift
i += 1
return value
def unBitShiftLeftXor(value, shift, mask):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff >> (32 - shift)) & 0xffffffff) << (i * shift)
part = value & part_mask
value ^= (part << shift) & mask
i += 1
return value
outputs = bytes.fromhex('641460a9e3953b1aaa21f3a2')
inputs = ''
for i in range(0, len(outputs), 4):
number = bytes_to_long(outputs[i:i+4])
number = unBitShiftRightXor(number, 19)
number = unBitShiftLeftXor(number, 17, 2245263360)
number = unBitShiftLeftXor(number, 9, 2029229568)
number = unBitShiftRightXor(number, 13)
inputs += hex(number)[2:].zfill(8)
print(inputs)
# 84b45f89af22ce7e67275bdc
|
由于这一题涵盖知识点过多,仅摘取其中涉及到随机数的部分。
lrlr.py文件:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
from Crypto.Cipher import AES
import random
# 略去50多行代码
def oldtest():
f=open("old","wb")
s=""
for i in range(1000):
s+=str(random.getrandbits(32))+"\n"
f.write(s)
# 略去10多行代码
oldtest()
# 略去1行代码
|
old文件:
3821224423
3496268056
2620561088
785910134
4160616763
4208721432
12680551
3267264049
2554408329
2185882337
2748782884
# .
# .
# .
# 一共1000个32bits随机数输出
用的是Python内置的random模块中的MT19937算法。
给了1000个连续的输出,我们可以利用前624个输出逆出初始的624个states。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
def unBitShiftRightXor(value, shift):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff << (32 - shift)) & 0xffffffff) >> (i * shift)
part = value & part_mask
value ^= part >> shift
i += 1
return value
def unBitShiftLeftXor(value, shift, mask):
i = 0
while i * shift < 32:
part_mask = ((0xffffffff >> (32 - shift)) & 0xffffffff) << (i * shift)
part = value & part_mask
value ^= (part << shift) & mask
i += 1
return value
def getState(number):
number = unBitShiftRightXor(number, 18) # reverse: tmp ^= (tmp >> 18)
number = unBitShiftLeftXor(number, 15, 0xefc60000) # reverse: tmp ^= (tmp << 15) & 0xefc60000
number = unBitShiftLeftXor(number, 7, 0x9d2c5680) # reverse: tmp ^= (tmp << 7) & 0x9d2c5680
number = unBitShiftRightXor(number, 11) # reverse: tmp ^= (tmp >> 11)
return number
def backtrace(numbers):
"""
Returns the initial state of the MT PRNG based on list of 624 output numbers
"""
assert(len(numbers) == 624)
state = []
for number in numbers:
state.append(getState(number))
return state
with open('old', 'r') as f:
numbers = [int(line.strip()) for line in f.readlines()]
states = backtrace(numbers[:624])
print(states)
# [3411300637, 2733702046, 3636981553, 3014539014, 146706710, 311936086, 726292125, 2045982456, 2643639630, 3881398749, 639365679, 2532971455, 1311802468, 4239048471, 3805504244, 4004772330, 3196421966, 3065172953, 578969822, 397235126, 1022258726, 197580289, 449224582, 2561406403, 264725192, 1730668657, ...]
|
进而可以根据这些states来构造random.setstate(states)的参数,设置我们的states与题目文件的一致,使得我们能够对后面的随机数输出进行预测。
1
2
3
|
# ...
init_state = (3, tuple(states + [624]), None)
random.setstate(init_state)
|
https://jazzy.id.au/2010/09/20/cracking_random_number_generators_part_1.html
https://jazzy.id.au/2010/09/21/cracking_random_number_generators_part_2.html
https://jazzy.id.au/2010/09/22/cracking_random_number_generators_part_3.html
https://jazzy.id.au/2010/09/25/cracking_random_number_generators_part_4.html
